La verticale geocentrica è la retta che congiunge un punto della superficie terrestre con il centro ideale della Terra. In ogni punto della superficie, essa forma un angolo rispetto alla verticale geodetica, chiamato angolo della verticale. Quest’ultimo ha una sola componente nord-sud e dipende matematicamente dalla latitudine geodetica: diventa zero ai poli e all’equatore, e diventa massima a $45^\circ$ di latitudine, con un valore di poco più di $11’$ e mezzo (valore che dipende dall’ ellissoide di riferimento scelto) ed è in genere molto più consistente rispetto alla deflessione della verticale, specialmente intorno alle latitudini $\pm45°$.
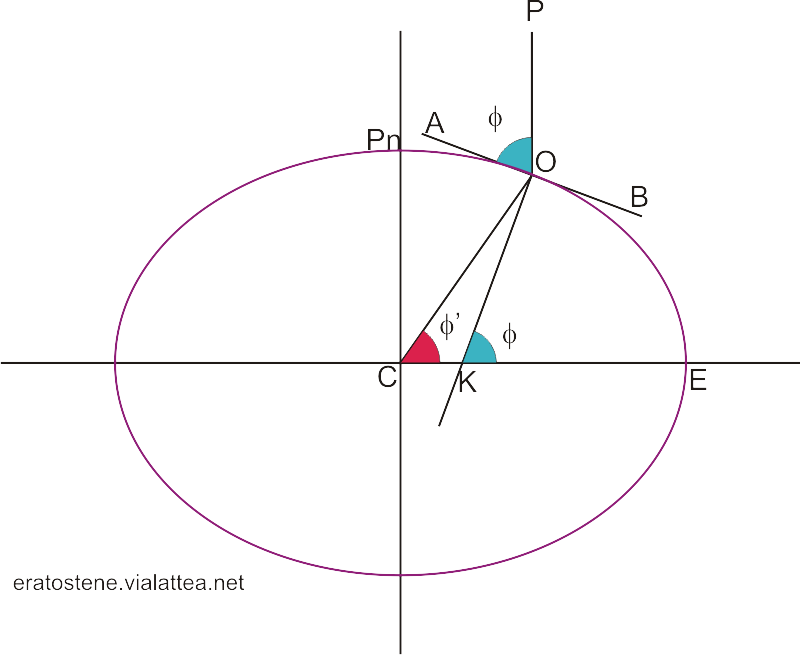
Qui è rappresentato l’ellissoide di riferimento.
$C$: il centro della Terra
$O$: un punto della superficie
$OK$: la verticale geodetica
$OC$: la verticale geocentrica
$P_n$: polo nord geografico
$PO$: la direzione del polo nord celeste
$AB$: piano tangente all’ellissoide per il punto $O$
$P_n C$: l’asse minore dell’ellissoide
$CE$: l’asse maggiore dell’ellissoide sul piano dell’equatore
$\hat{OKE}$: latitudine geodetica ($\phi$), cioè l’angolo tra la verticale geodetica e il piano dell’equatore
$\hat{OCE}$: latitudine geocentrica ($\phi’$), cioè l’angolo formato dalla verticale geocentrica con l’equatore
COK: angolo della verticale
L’angolo della verticale è uguale alla differenza tra $\phi$ e $\phi’$.
Si nota che per latitudini intermedie, tra il polo nord e l’equatore, $\phi$ è sempre maggiore di $\phi’$.
In maggior dettaglio, l’angolo alla verticale $V$ alle varie latitudini, si può calcolare in funzione di $\phi$ con la seguente formula (Jean Meeus, Astronomical Algorithms, 1999):
$$V=\text{692,73}^{”} \sin \left(2\phi\right)-\text{1,16}^{”}\sin\left(4\phi\right)$$
Si nota che $\sin\left(2\phi\right)$ è un valore compreso tra $0$ e $1$; vale $1$ se $\phi=45^\circ$ e vale zero se $\phi=90^\circ$ oppure $\phi=0^\circ$.