Il quadrato delle ombre è un antico calcolatore analogico di tangenti, strettamente legato all’uso dello gnomone. Esso simulava l’ombra di uno gnomone verticale (umbra recta) e, contemporaneamente quella di uno gnomone verticale (umbra versa).

Il quadrante del 1568, firmato da Giovanni Battista Giusti, artigiano costruttore di strumenti scientifici, presenta un quadro delle ombre con scala duodecimale. Lo strumento è conservato al Museo Galileo di Firenze.

Sempre al Museo Galileo di Firenze è conservato questo astrolabio di Johann Richter (Altdorf, 1591) il cui retro presenta due quadrati delle ombre con scala duodecimale.
Il matematico e astronomo austriaco Georg von Peurbach (1423-1461) codificò lo strumento nel suo trattato Quadratum Geometricum, ma la sua origine è più antica, legata all’uso dello gnomone.
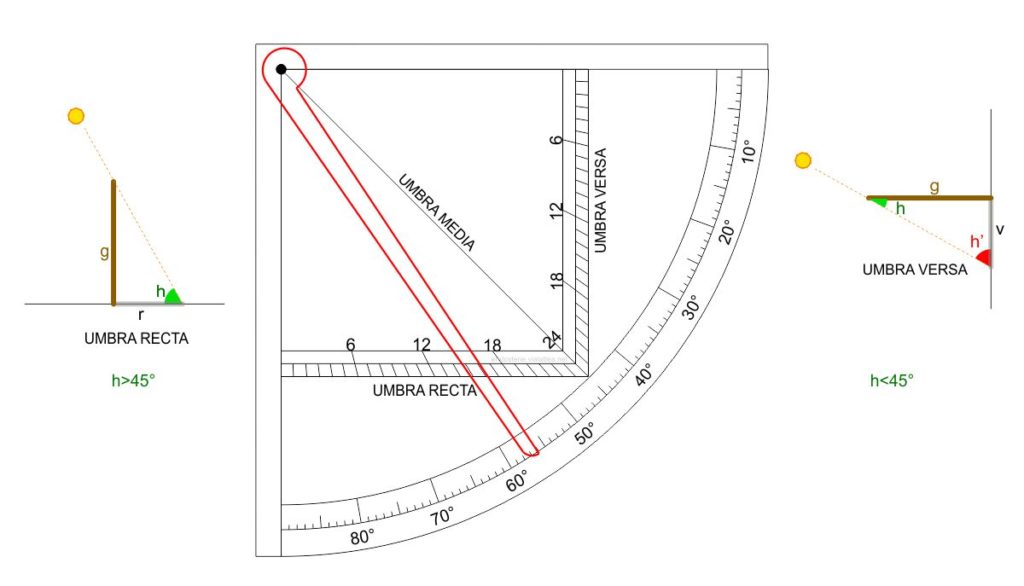
Il quadrato delle ombre è essenzialmente un quadrato con due lati graduati, generalmente suddivisi in 12, 24 o 48 tacche. La scala orizzontale simula l’ombra proiettata su un piano orizzontale da uno gnomone verticale e per questo motivo è chiamata UMBRA RECTA.
La scala verticale invece simula l’ombra proiettata da uno gnomone orizzontale su una parete verticale; di qui il suo nome UMBRA VERSA. La lancetta, un’alidada spesso dotata di pinnule forate e di due mirini, era adatta per essere allineata con i raggi solari o con un oggetto di osservazione. Essa mette in corrispondenza un valore della scala esterna in gradi con un valore delle umbrae.
La scala esterna graduata da $0^\circ$ a $90^\circ$ indica l’angolo di inclinazione dei raggi solari rispetto al piano orizzontale, cioè l’altezza del Sole, che qui abbiamo rappresentato con l’angolino di colore verde $h$. Si noti che l’angolino $h’$, colorato di rosso è il complementare di $h$ e quindi è la distanza zenitale del Sole. Perciò:
$$h’=90^\circ-h$$
Sia la scala dell’umbra recta che quella dell’umbra versa, in questo caso, sono lunghe $24$ unità. E’ poco importante di che unità si tratti perché ciò che conta è che lo gnomone sia immaginato lungo $24$ unità.
Lo strumento permette una lettura diretta delle funzioni tangente e cotangente. Se $h$, letto sulla scala esterna, è maggiore di $45^\circ$, esso corrisponde ad un valore $r$ letto sull’umbra recta. Come abbiamo detto, lo gnomone $g$ è lungo $24$ unità, perciò:
$$\frac{g}{r}=\frac{24}{r}=\tan{h}$$
Se $h$ è minore di $45^\circ$, conviene utilizzare il suo complementare $h’=90^\circ-h$ perché l’alidada va a incontrare l’umbra versa. In questo caso:
$$\frac{g}{v}=\frac{24}{v}=\tan{h’}=\frac{1}{\tan{h}}=\cot{h}$$
In sintesi, le due formule utili sono le seguenti, rispettivamente la prima per l’umbra recta e la seconda per l’umbra versa:
$$\boxed{\tan{h}=\frac{g}{r}}$$
$$\boxed{\tan{h}=\frac{v}{g}}$$
Se l’angolo $h$ è uguale a $45^\circ$, è l’umbra media: $g=v=r$ e quindi $\frac{g}{r}=\tan{h}=\cot{h}=1$: lo gnomone proietta un’ombra è uguale a sé.
Senza disturbare la trigonometria, si può trattare il quadrato delle ombre come uno strumento che sfrutta la similitudine tra due triangoli rettangoli e tutto si risolve con le adeguate proporzioni. Se si allinea l’alidada con i raggi solari, il rapporto tra $g=24$ e il valore letto su una delle due umbrae è in relazione con il rapporto tra l’altezza di un edificio $A$ e la lunghezza della sua ombra simultanea $B$.
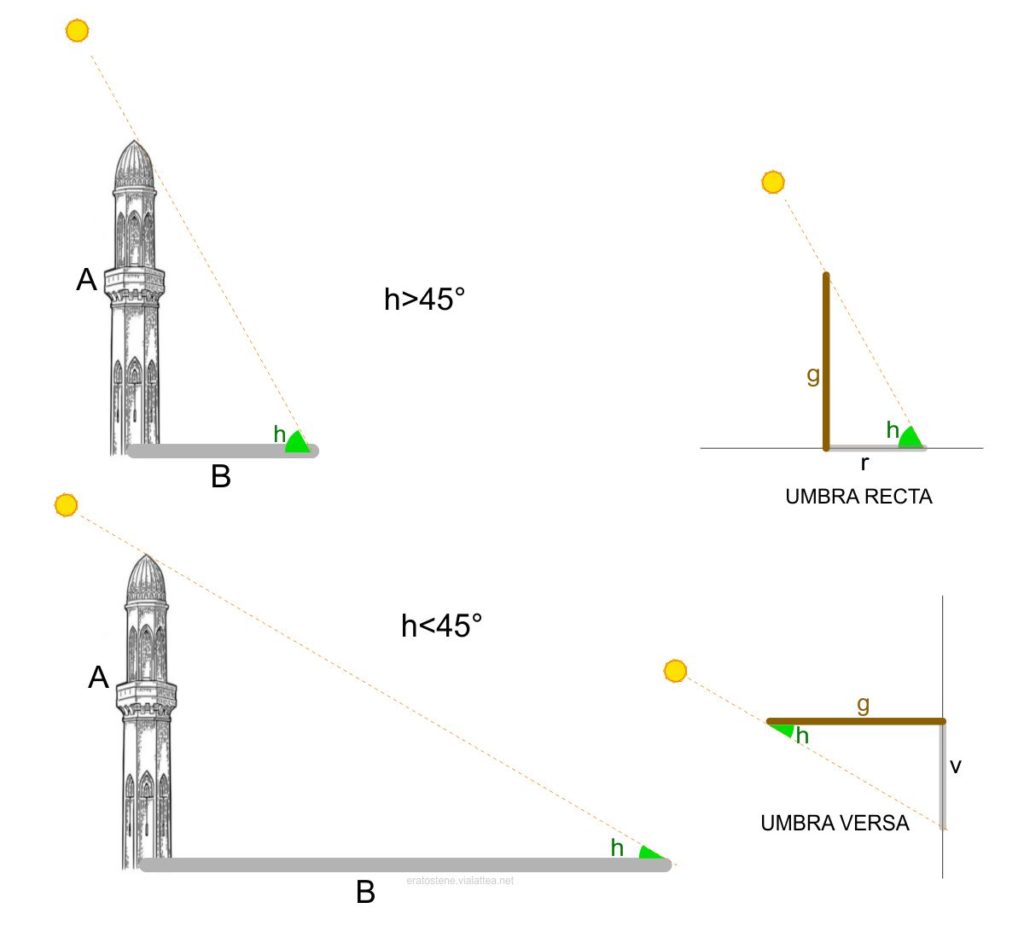
Se $h>45^\circ$ si legge $r$ sull’umbra recta:
$$\boxed{\frac{A}{B}=\frac{g}{r}}$$
Se $h<45^\circ$ si legge $v$ sull’umbra versa:
$$\boxed{\frac{A}{B}=\frac{v}{g}}$$
Il quadrato delle ombre è di facile costruzione: le scale delle umbrae si possono impostare a piacere; maggiore il numero di tacche, maggiore è la precisione che si ottiene (una scala decimale forse è più adatta alle nostre abitudini). Può essere disegnato su un quadrante fisso o mobile, a seconda dell’uso che se ne può fare. Un quadrante fisso va associato ad un’alidada mentre il quadrante mobile va dotato di un filo a piombo.
Vediamo alcuni esempi di problemi pratici, astronomici o puramente geometrici, risolti con il quadrato delle ombre.
PROBLEMA 1
Ad una certa ora del giorno, una torre proietta un’ombra lunga 26 metri. L’altezza del Sole, misurata con l’alidada, indica $56^\circ$. Quanto è alta la torre?
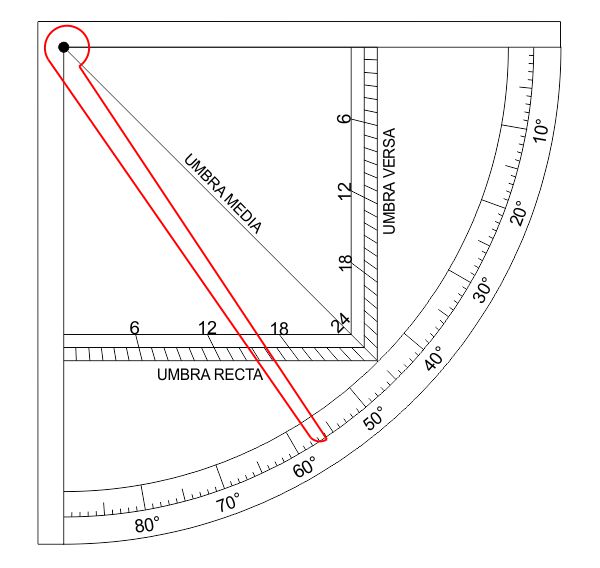
L’angolo $h$ è minore di $45^\circ$ perciò si legge $r$ sulla scala dell’umbra recta che indica il valore $16$. Perciò:
$$\frac{A}{B}=\frac{g}{r}$$
$$\frac{A}{26m}=\frac{24}{16}$$
$$A=26m\cdot\frac{24}{16}=39m$$
La torre è alta 39 metri.
PROBLEMA 2
Un edificio proietta un’ombra lunga 44 metri e il quadrato delle ombre misura contemporaneamente $19°$ di altezza del Sole. Quanto è alto l’edificio?
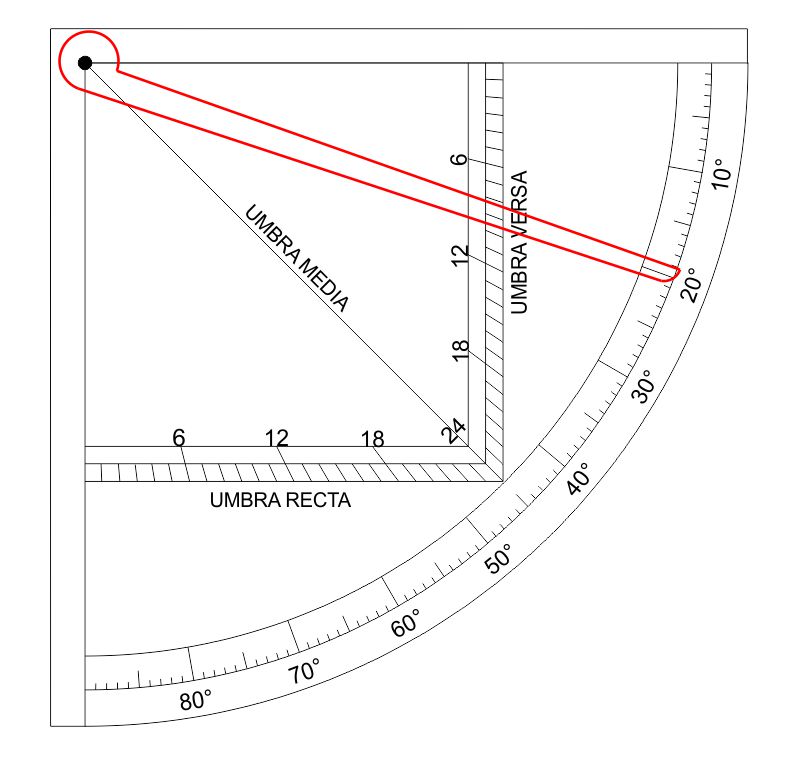
In questo caso l’altezza del Sole $h$ è minore di $45^\circ$, perciò si legge $v$ sulla scala dell’umbra versa che indica il valore $8$:
$$\frac{A}{B}=\frac{v}{g}$$
$$\frac{A}{44m}=\frac{8}{24}$$
$$A=44m\cdot\frac{8}{24}=14,6m$$
L’edificio è alto circa 14 metri e mezzo.
PROBLEMA 3
Un bastone alto $150 cm$ proietta un’ombra lunga $125cm$. Qual’è l’altezza del Sole?
In questo caso non si usa il quadrato delle ore per misurare ma per eseguire un calcolo trigonometrico. Si procede calcolando il valore $r$ dell’umbra recta. Infatti, se l’altezza del bastone è maggiore della sua ombra, l’altezza del Sole è maggiore di $45^\circ$:
$$\frac{A}{B}=\frac{g}{r}$$
$$\frac{150m}{125m}=\frac{24}{r}$$
da cui:
$$r=24\cdot\frac{125}{150}=20$$

A questo punto si allinea l’alidada sul valore $20$ dell’umbra recta e si trova il corrispondente valore in gradi dell’altezza del Sole sulla scala graduata: $h=50^\circ$.
PROBLEMA 4
Un bastone alto $150 cm$ proietta un’ombra lunga $180 cm$. Qual’è l’altezza del Sole?
E’ un problema molto simile al precedente ma, in questo caso si utilizza l’umbra versa perché l’altezza del Sole è minore di $45^\circ$. Perciò:
$$\frac{A}{B}=\frac{v}{g}$$
”$$\frac{150cm}{180cm}=\frac{v}{24}$$
$$v=\frac{150}{180}\cdot24=20$$
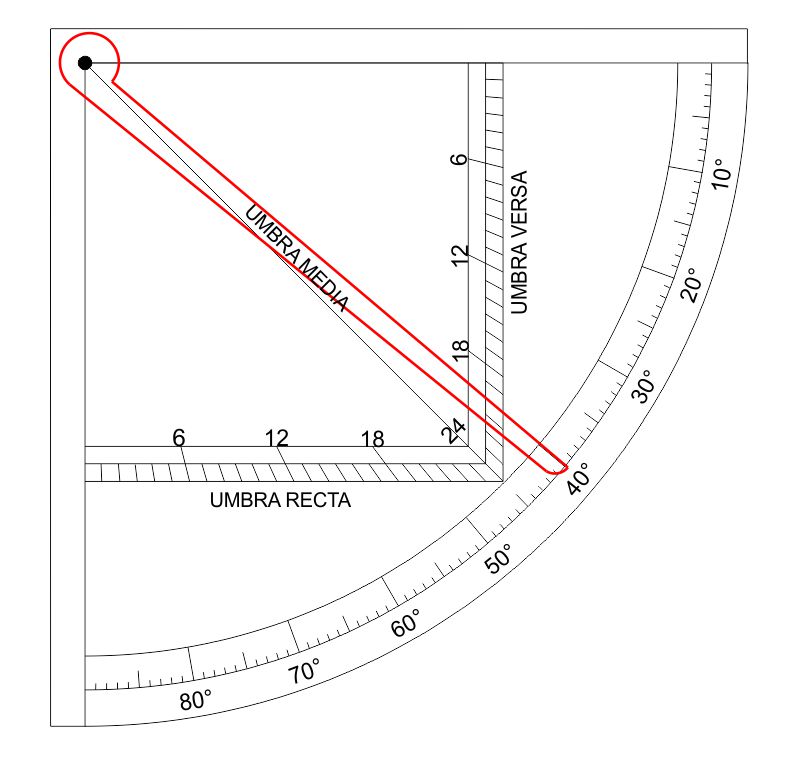
Si posiziona l’alidada sul valore $20$ dell’umbra versa e si ottiene il corrispondente valore in gradi dell’altezza del Sole: $h=40^\circ$
PROBLEMA 5
Quanto vale la tangente di $74^\circ$?
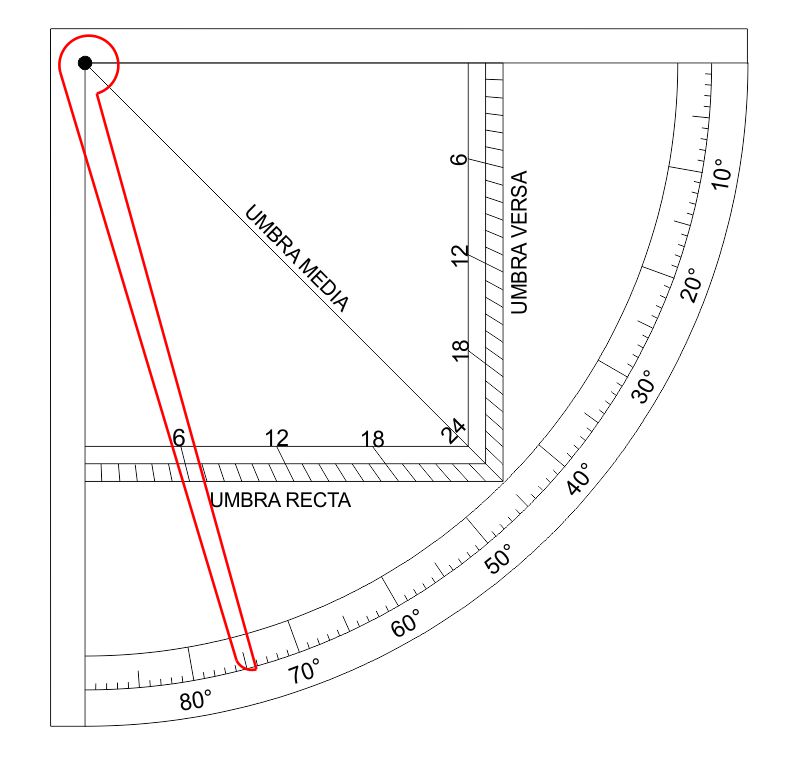
A differenza dei problemi precedenti, in questo caso e nei prossimi, il quadrato delle ombre è usato come calcolatore analogico tascabile, non più come strumento di misura. Si posiziona l’alidada sui $74^\circ$ e si legge il valore $r=7$ sulla scala dell’umbra recta.
Il valore della tangente di $74^\circ$ si ottiene da una semplice divisione. Dato che nell’umbra recta vale la relazione:
$$\tan{h}=\frac{g}{r}$$
$$\tan 74^\circ = \frac{24}{7}=3,4$$
PROBLEMA 6
Quanto vale la tangente di $12^\circ$?
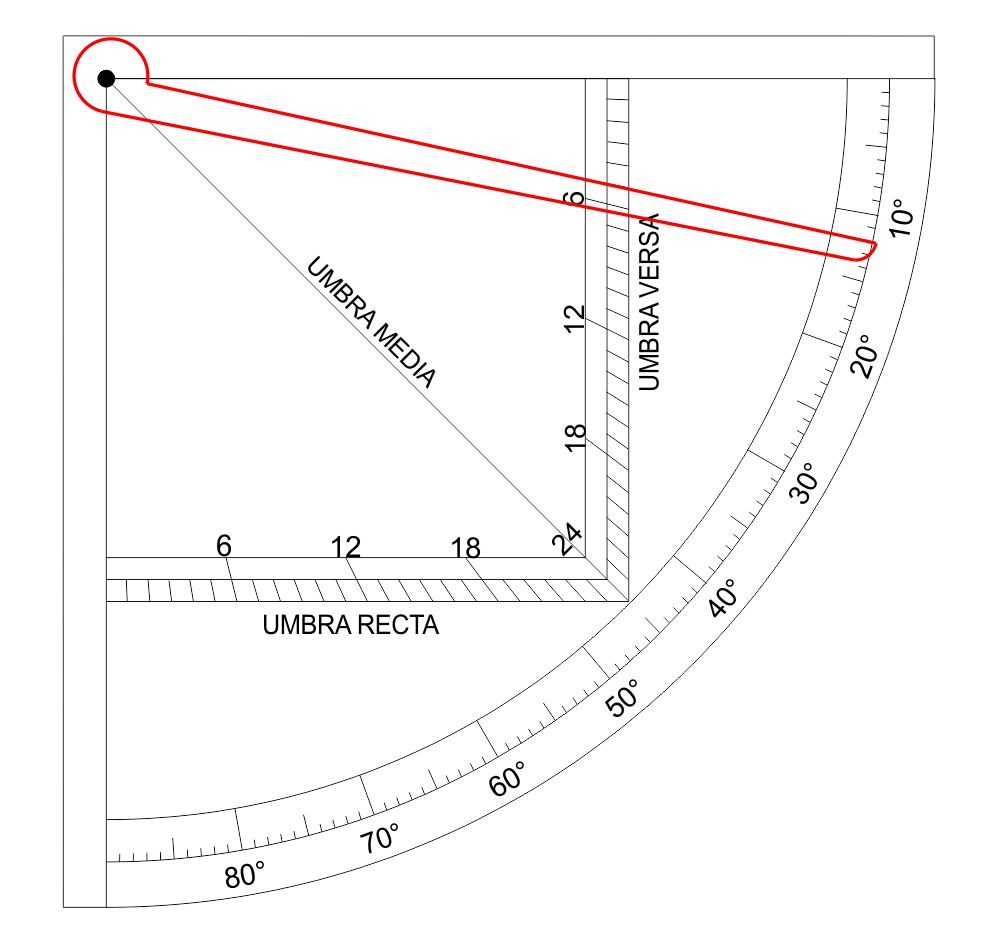
In corrispondenza ai $12^\circ$ si legge il valore $v=5$ sull’umbra versa. Perciò:
$$\tan{h}=\frac{v}{g}$$
$$\tan{12^\circ}=\frac{5}{24}=0,2$$
PROBLEMA 7
La tangente di un angolo è $0,75$. Quanto vale l’angolo?
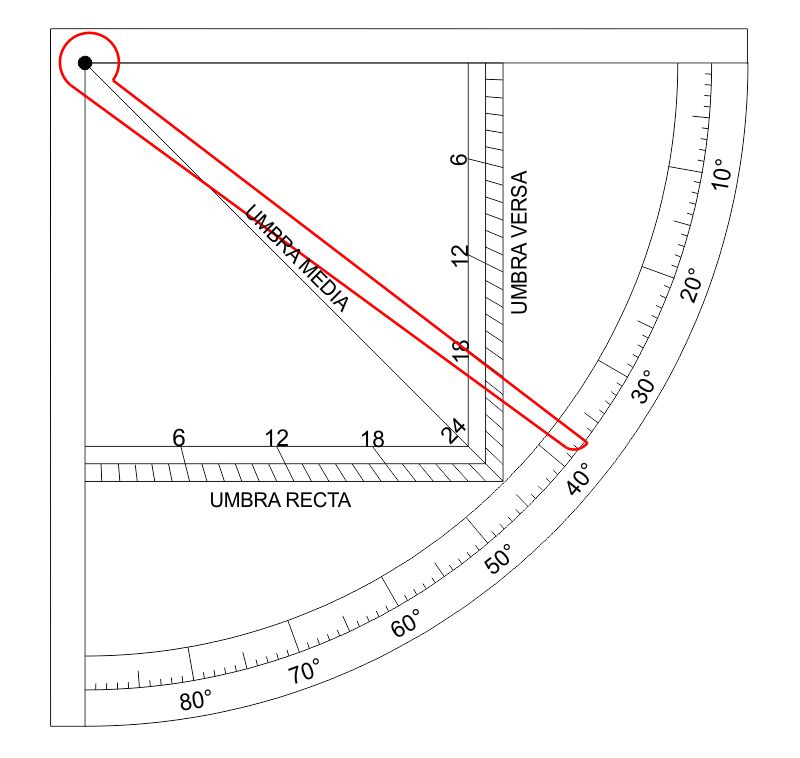
In questo caso usiamo il quadrato delle ombre come calcolatore della funzione arcotangente. Il valore della tangente è minore di $1$ perciò si utilizza la formula dell’umbra versa:
$$\tan{h}=\frac{v}{g}$$
Da cui si ricava $v$:
$$v=0,75\cdot24=18$$
Ora si allinea l’alidada sul valore $18$ della scala dell’umbra versa e si ottiene la corrispondenza dei $37^\circ$ sulla scala graduata esterna. Perciò:
$$\arctan{0,75} = 37^\circ$$

