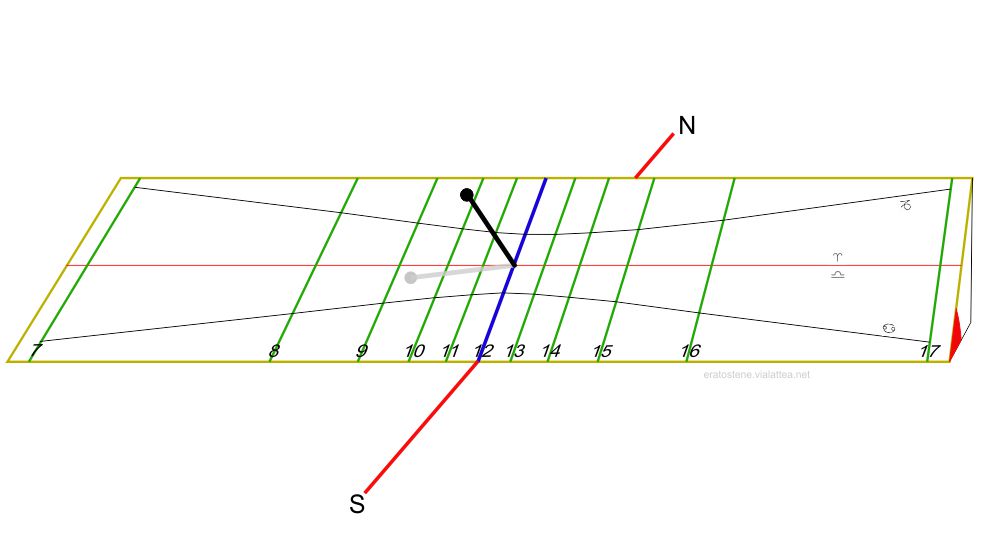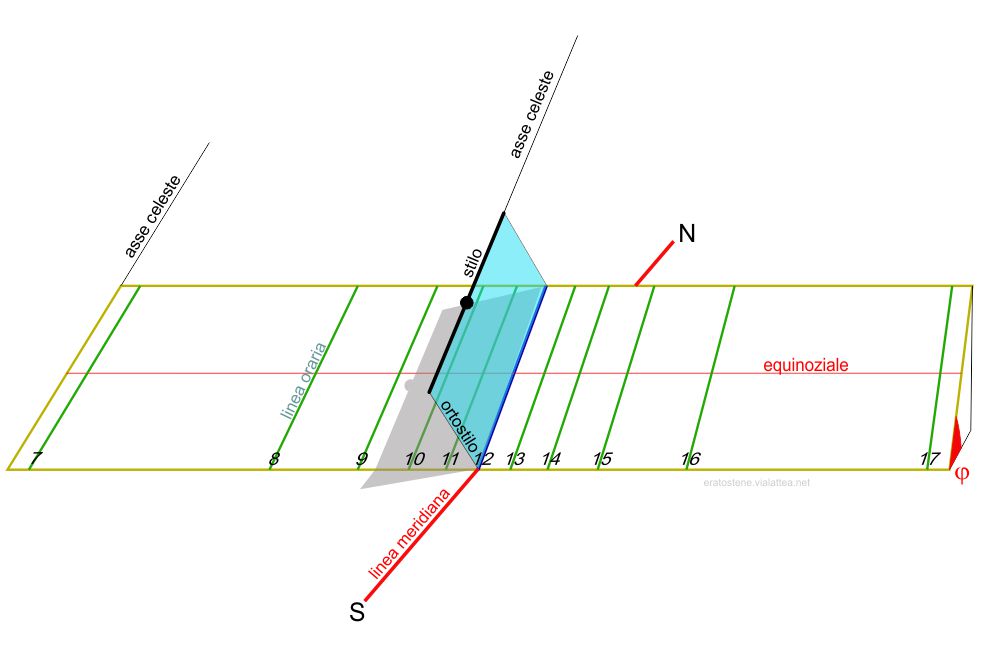
E’ un orologio solare molto semplice da capire e da costruire. Il quadrante è un rettangolo inclinato rispetto all’orizzonte di un angolo $\varphi$ pari alla latitudine. Il lato maggiore del quadrante è allineato con la linea est-ovest (o linea equinoziale). In questo modo, l’asse celeste si trova sul piano del quadrante il quale coincide con il piano del primo orario. Lo stilo è disposto nella direzione dell’asse celeste. Si tratta perciò uno stilo polare. Esso è parallelo al piano del quadrante ed è separato da esso da una distanza importante (l’ortostilo). Le linee orarie sono tutte parallele tra loro e l’ampiezza complessiva della serie di linee orarie dipende dalla lunghezza dell’ortostilo: quanto più grande è la distanza tra lo stilo e il piano del quadrante, tanto maggiore è la distanza tra le linee orarie.
L’orologio possiede due simmetrie assiali: la principale ha come asse la linea oraria che si trova sotto lo stilo (sottostilo). E’ la linea oraria delle ore $12$. Tutte le altre linee orarie, le mattutine a ovest e le pomeridiane a est, si dispongono simmetricamente rispetto a questa. L’ombra dello stilo si proietta sul piano del quadrante parallelamente alle linee orarie e la sua posizione rispetto ad esse indica l’ora solare. L’altra simmetria, meno importante, ha come asse l’equinoziale disegnata lungo i punti medi delle linee orarie. Il pallino, o ingrossamento, al centro dello stilo è opzionale ma segna questa seconda simmetria. Sia il pallino che la linea equinoziale descritta, si trovano sul piano dell’equatore celeste. Se l’ombra del pallino si trova al di sotto della linea equinoziale, significa che il Sole si trova nell’emisfero celeste nord e la sua declinazione è positiva: siamo nel periodo dell’anno compreso tra l’equinozio di marzo e quello di settembre. Se l’ombra del pallino è al di sopra dell’equinoziale, il Sole si trova nell’emisfero celeste sud, la sua declinazione è negativa e ci troviamo nel periodo compreso tra l’equinozio di settembre e quello di marzo. Dalla figura precedente si evince che sono all’incirca le ore $9:20$ solari e che la declinazione del Sole è positiva. Come è facile capire, il rettangolino azzurro, in sé, non è necessario. E’ stato rappresentato per migliorare la comprensibilità dello schema. Normalmente si usa il solo stilo polare sostenuto in vari modi, oppure il solo rettangolino sottostante il cui lato parallelo al quadro fa le veci dello stilo.
Per posizionare il quadrante si traccia innanzitutto la linea meridiana con uno dei metodi proposti, Si disegna quindi la linea est-ovest perpendicolare ad essa. Quest’ultima è la linea guida per orientare il lato maggiore del quadrante. Esso va sostenuto in qualche modo per formare l’angolo $\varphi$ rispetto al piano orizzontale.
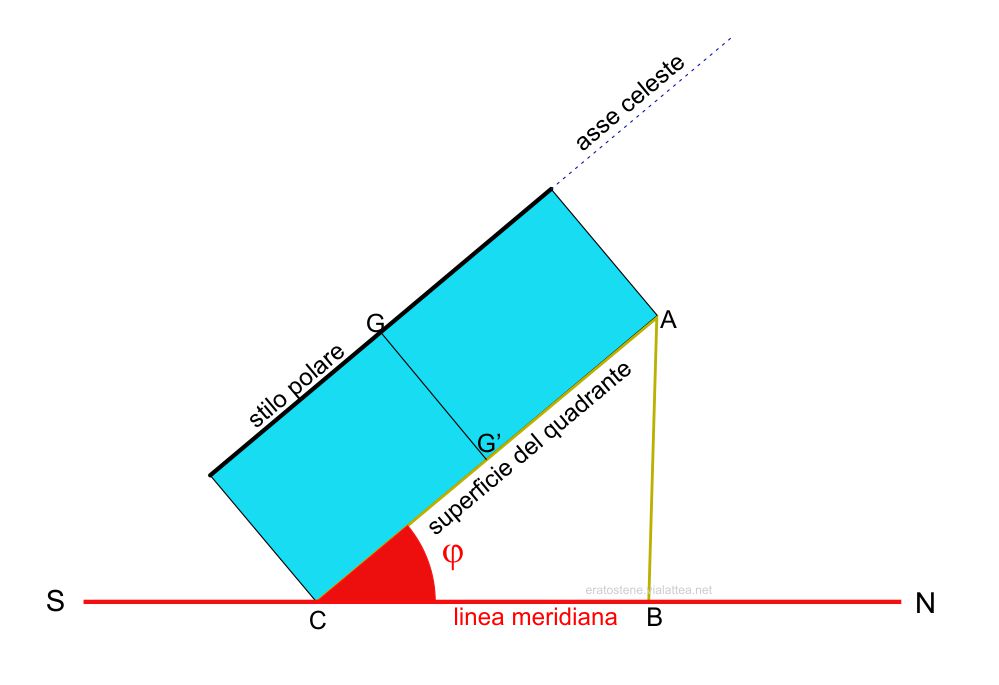
L’orologio solare qui è visto lateralmente. L’ortostilo, distanza tra lo stilo e la superficie del quadrante, è il segmento $GG’$. Per un lavoro di precisione è conveniente usare una semplice regola trigonometrica per calcolare il triangolo “di sostegno” $ABC$ che permetta la giusta inclinazione del quadrante. Dati la misura del’altezza $\overline{CA}$ del quadrante e della latitudine $\varphi$:
$$\overline{CB}=\overline{CA}\cos\varphi$$
$$\overline{AB}=\overline{CA}\sin\varphi$$
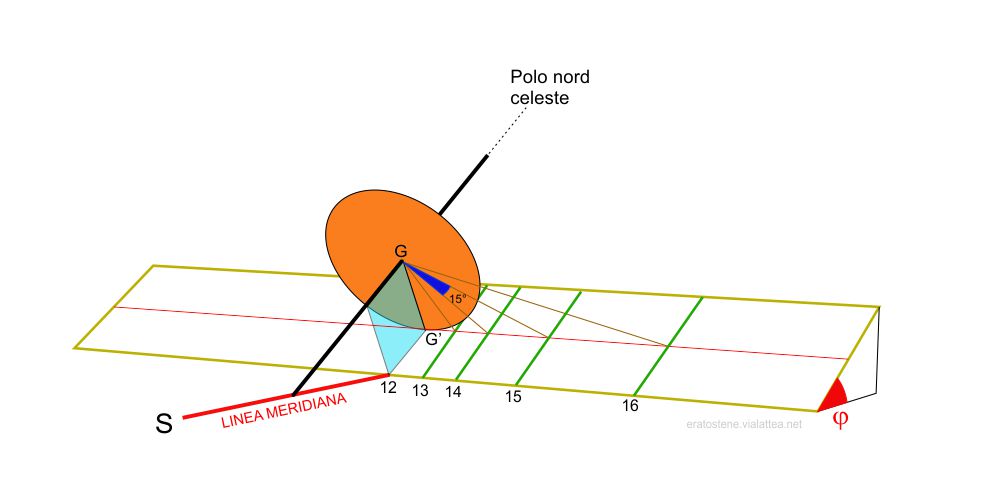
Per capire il funzionamento del quadrante polare, ci rifacciamo all’orologio equatoriale. Immaginiamolo posizionato come in figura. Il suo stilo coincide con lo stilo dell’orologio polare. Il suo quadrante circolare ha come raggio la distanza $GG’$, cioè l’ortostilo. In questo modo, il quadrante equatoriale tocca la superficie del quadrante polare nel punto centrale $G’$. Se si prolungano le linee orarie dell’orologio equatoriale, esse intersecano il piano del quadrante polare in alcuni punti lungo l’equinoziale. Distanziando tra loro di $15^\circ$ le linee orarie dell’equatoriale partendo dalle $12$, si ottengono i punti per ogni ora intera.
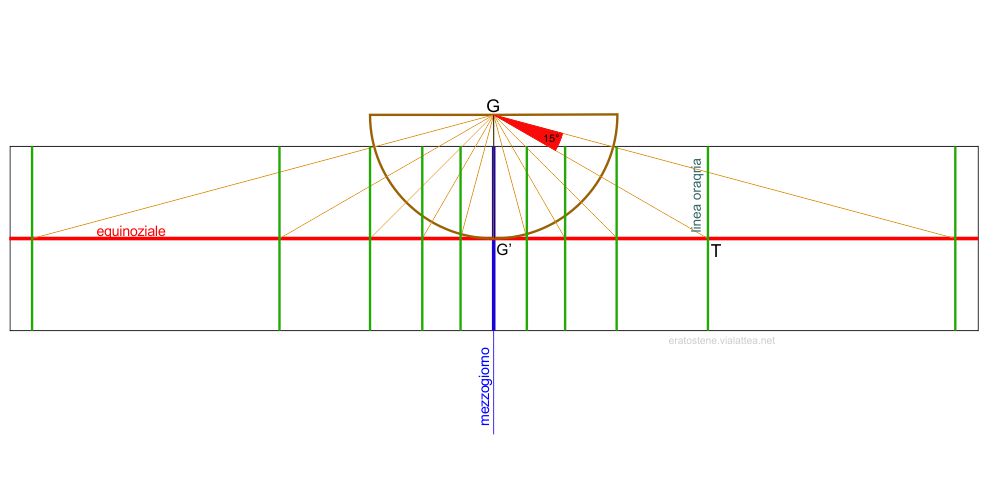
Se ribaltiamo idealmente il quadrante equatoriale sul piano del quadrante polare, otteniamo la figura qui a fianco, utile per la costruzione grafica. Da notare il raggio $GG’$ del cerchio che dev’essere uguale all’ortostilo. Prolungando una linea oraria si raggiunge l’equinoziale (ad esempio $GT$) e da quel punto di intersezione si traccia la linea oraria.
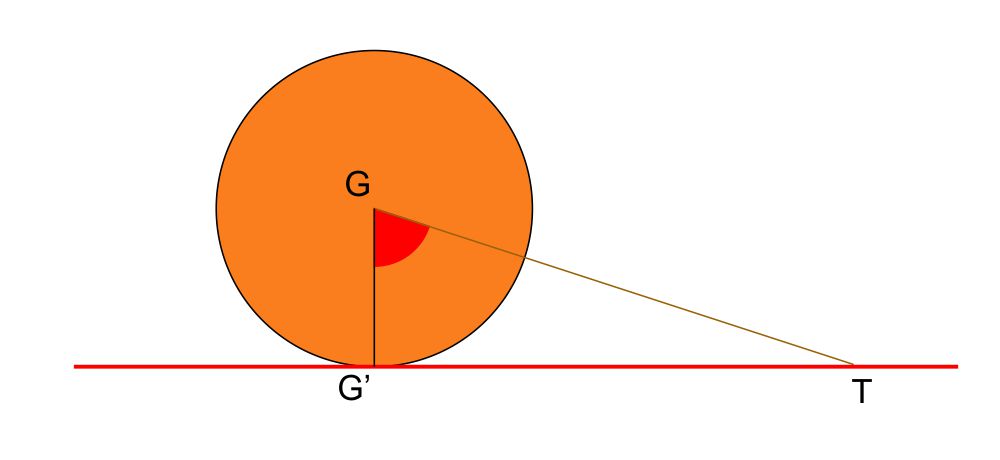
Chi desidera privarsi delle delizie delle costruzioni grafiche a favore di un disegno più preciso può ricorrere ad una semplicissima trigonometria e calcolare la distanza $\overline{G’T}$ partendo dalla misura dell’ortostilo $\overline{GG’}$ e dal valore dell’angolo orario $G’\hat{G}T=\alpha$ espresso in gradi corrispondente alla differenza $h$ espressa in ore tra l’ora della linea oraria da rappresentare e il mezzogiorno.
$h=16-12$ differenza dal mezzogiorno, in ore
$G’\hat{G}T=\alpha = h\times15^\circ$
Infine usiamo la funzione tangente per calcolare la distanza cercata:
$\overline{G’T}=\overline{GG’}\cdot \tan{\alpha}$
Ad esempio, per calcolare la linea oraria delle ore $16$ solari che corrispondono ad una differenza di $4$ ore dal mezzogiorno, si procede in questo modo:
$h=16-12$ differenza dal mezzogiorno, in ore
$G’\hat{G}T=\alpha = h\times15^\circ$
Infine usiamo la funzione tangente per calcolare la distanza cercata:
$\overline{G’T}=\overline{GG’}\cdot \tan{\alpha}$
Si usa lo stesso valore calcolato qui per tracciare anche la linea oraria delle ore $8$ che è simmetrica a quella delle ore $16$.
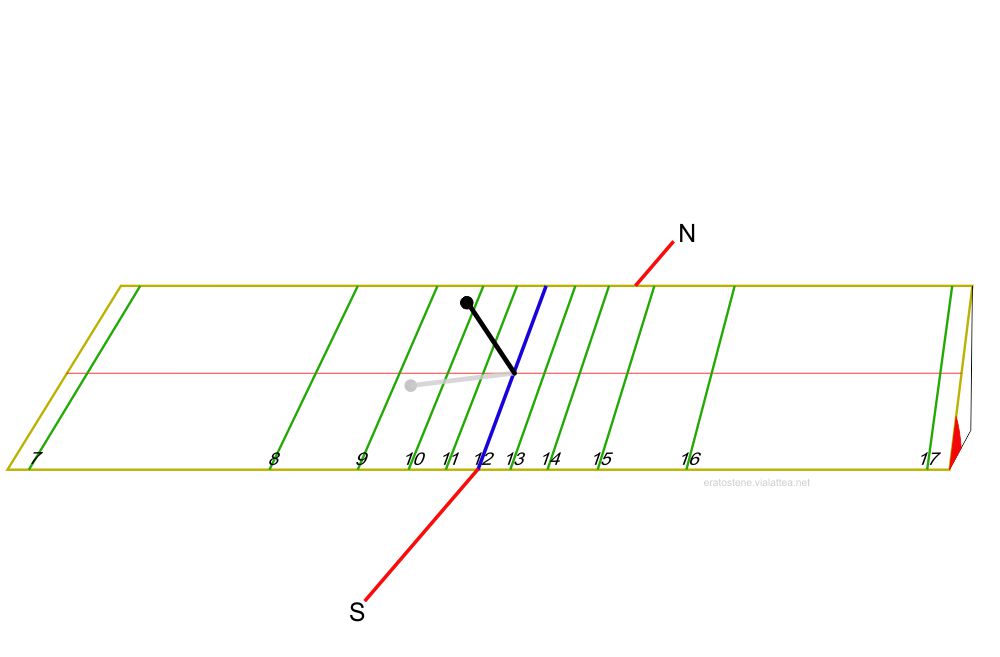
Una variante di costruzione ancora più agevole consiste nell’usare uno stilo perpendicolare al quandrante la cui lunghezza è uguale all’ortostilo. L’ombra dell’apice dello stilo (in questo caso la pallina) indica l’ora e anche il segno della declinazione solare.

Qui a fianco un semplicissimo modellino in cartone di orologio polare con uno stuzzicadente come stilo disposto come nella variante descritta qui sopra. La punta dell’ombra segna l’ora sulle linee orarie parallele. Sono ancora visibili le linee di costruzione che possono essere cancellate. L’orologio segna all’incirca le ore $8:45$ solari di una data con declinazione solare negativa.
I più pignoli possono completare l’orologio aggiungendo alcune linee orarie. Lo si può fare se lo stilo polare possiede un segnalino centrale nel punto $G$, come ad esempio un anello o un rigonfiamento, oppure se si utilizza uno stilo perpendicolare al piano del quadrante, come nel modello precedente. Una linea oraria descrive il percorso della proiezione dell’apice dello stilo (o meglio del punto $G$) sul piano nel corso di una giornata ed è diversa di giorno in giorno. La linea oraria dei giorni degli equinozi è la retta equinoziale. Se la declinazione del Sole è negativa, la linea oraria è una conica che si trova al di sopra dell’equinoziale, con la concavità verso l’alto, e viceversa.
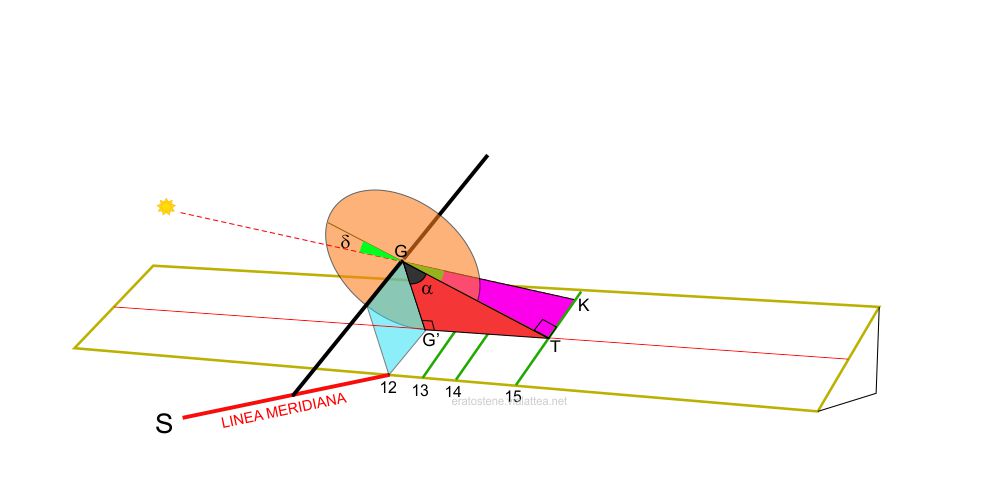
Proviamo ad analizzare una situazione specifica. Nella rappresentazione qui a fianco sono le ore $15$ solari e il Sole ha una declinazione $\delta$ negativa. Il raggio di luce che parte dal centro del disco solare e giunge al punto $G$ si trova al di sotto del piano equatoriale (indicato dal cerchio del quadrante equatoriale) e forma con esso un angolo $\delta$. Il raggio prosegue poi al di sopra del piano equatoriale e giunge nel punto $K$ della linea oraria delle ore $15$. Se fossero le ore $15$ di un giorno equinoziale, $\delta$ sarebbe uguale a zero e il raggio di luce raggiungerebbe il punto $T$ della stessa linea oraria.
Abbiamo già visto prima come calcolare la distanza $\overline{G’T}$:
$\overline{G’T}=\overline{GG’}\cdot \tan{\alpha}$
Si vuole risolve ora il triangolo rettangolo $GTK$, retto in $T$, che ha il lato $GT$ in comune con il precedente triangolo $GG’T$. Lo scopo è calcolare la distanza $\overline{KT}$ per poter segnare il punto della linea oraria. Perciò si calcola per primo il lato $GT$ utilizzando la funziona coseno sul triangolo $GG’T$
$\overline{GT}=\frac{\overline{GG’}}{\cos\alpha}$
Ora possiamo finalmente calcolare $\overline{TK}$ applicando la funzione tangente sul triangolo $GTK$:
$\overline{TK}=\overline{GT}\tan \delta$
Per semplificare, chiamando $g$ l’ortostilo $GG’$, si può riassumere in un’unica formula il calcolo di $\overline{TK}$:
\begin{equation}
\boxed{\overline{TK}=g\frac{\tan \delta}{\cos \alpha}}
\end{equation}
Per tracciare le due linee diurne solstiziali basta porre $\delta=23^\circ\!\text{,5}$ e completare il calcolo per i pochi punti pomeridiani del solstizio di dicembre. Grazie alla doppia simmetria assiale dell’orologio (di cui si accennava prima) è facilissimo completare la parte sinistra e poi l’intera linea solstiziale di giugno senza eseguire altri calcoli.
Chi invece è più tradizionalista e non rinuncia al piacere di usare squadra e compasso, ecco come trasformare in metodo grafico le operazioni trigonometriche descritte:

Vediamo come esempio la ricerca del punto $K$ di un’ora pomeridiana del solstizio di dicembre, premettendo che il triangolo $GG’T$ sia già stato costruito correttamente. Si costruisce ora il triangolo rettangolo $GTK’$ con le seguenti operazioni:
1) tracciare la semiretta $TT’$ perpendicolare a $GT
2) misurando un angolo $\delta=23^circ\!\text{,5}$ in $G$ adiacente all’angolo $\alpha$, si traccia una semiretta che interseca $TT’$ nel punto $K’$. Il segmento $TK’$ è la distanza cercata per trovare la posizione di $K$, perciò:
3) si traccia un arco di circonfereza puntando con il compasso in $T$ e aprendo un raggio $TK’$. Tale arco interseca la linea oraria di $T$ nel punto $K$.
Congiungendo tutti i punti $K$ tra loro si ottiene una spezzata che rappresenta la conica della linea diurna. Il risultato finale assomiglierà a questo, dove il simbolo Capricorno ![]() indica la linea diurna del solstizio di dicembre, il simbolo Cancro
indica la linea diurna del solstizio di dicembre, il simbolo Cancro ![]() indica quella del solstizio di giugno e i due simboli di Ariete
indica quella del solstizio di giugno e i due simboli di Ariete ![]() e Bilancia
e Bilancia ![]() indicano l’equinoziale:
indicano l’equinoziale: