Indice
< Gli archi visibili delle stelle
> La ricerca degli equinozi
In questa pagina impariamo ad eseguire la misura dell’inclinazione dell’asse celeste rispetto al piano dell’orizzonte. L’asse celeste è un asse ideale il cui assetto deve essere dedotto in base al moto apparente diurno della sfera celeste.
Con l’impiego di strumenti semplici, la misurazione dell’altezza del polo celeste non è tra le più facili. Gli attuali abitanti dell’emisfero boreale sono facilitati dalla presenza di una stella molto vicina al polo celeste nord nota come stella polare (Polaris o $\alpha$ Ursae Minoris). Questa stella, infatti, ad una prima osservazione sembra sempre immobile con il passare delle ore, ma anche con il passare dei giorni e degli anni. La sua altezza e il suo azimut non sembrano variare. Abbiamo l’impressione che essa rappresenti il centro di rotazione delle stelle circumpolari. Questo fatto ci potrebbe far pensare che la stella polare si trovi esattamente nel polo nord celeste. In realtà, un’osservazione più attenta ci permette di scoprire che anch’essa compie il suo moto circolare apparente assieme alla sfera celeste, attorno ad un punto che dista meno di un grado. Se ci accontentiamo di un errore di un grado e mezzo circa, possiamo eseguire semplicemente la misura dell’altezza della stella Polaris. Se invece desideriamo ottenere una stima più accurata dovremo basarci sulla geometria dei moti apparenti delle stelle circumpolari ed eseguire molte misurazioni.
Usando la stella polare è sufficiente una sola misurazione a qualsiasi ora della notte e in qualsiasi stagione dell’anno. Possiamo usare un rudimentale quadrante mobile come descritto qui. E’ un tubicino al quale è fissato un goniometro e un filo a piombo. Traguardando la stella polare attraverso il tubicino, si può leggere l’altezza indicata dal filo a piombo. Un quadrante fisso dotato di mirino renderebbe la misura più agevole.
Una maggior precisione si ottiene misurando le altezze delle culminazioni delle stelle circumpolari. Per rispettare il nostro approccio “primitivo”, suggerisco di usare il metodo del merkhet.

Le stelle circumpolari, come abbiamo visto, percorrono moti circolari antiorari concentrici attorno al polo nord celeste. Di conseguenza la direzione dell’asse celeste è la bisettrice tra le direzioni dei passaggi sopra il polo e sotto il polo di una stessa stella.
E’ necessario perciò misurare le due altezze di una stessa stella nei due momenti in cui essa transita al meridiano celeste al di sopra del polo (culminazione superiore) e al di sotto di esso (culminazione inferiore).

Si sceglie una stella facilmente riconoscibile, che si trovi nei pressi del meridiano inferiore, cioè al di sotto della stella Polare, e che stia per attraversare il piano meridiano. Data la sua rotazione antioraria, questa stella si troverà ancora nell’emisfero occidentale ma a piccola distanza dal meridiano inferiore. Traguardando il filo a piombo, si attende finché la stella si allinea ad esso. In quel momento si sposta il segnalino, come descritto nella pagina citata, e si raccolgono i dati per calcolare l’altezza.
La stessa stella attraverserà il meridiano superiore in un altro istante di tempo che è prevedibile anche per mezzo di alcune semplici regole. Dato che la rotazione completa avviene in 24 ore circa, la stella attraverserà il meridiano superiore dopo 12 ore dalla culminazione inferiore. Così, in una notte invernale si possono eseguire entrambe le misurazioni, la prima dopo il tramonto e la seconda prima dell’alba. In ogni caso, il transito al meridiano di una stella avviene con un anticipo di circa 4 minuti per ogni notte successiva. Inoltre, a distanza di 6 mesi dalla culminazione inferiore ritroviamo, alla stessa ora, un suo transito al meridiano superiore.
Una volta ottenute entrambe le altezze, $h_1$ relativa alla culminazione inferiore e $h_2$ a quella superiore, l’altezza $\varphi$ del polo celeste si calcola con la semplice formula:
$$\varphi = \frac{h_2-h_1}{2}$$
Abbiamo già considerato circolo massimo dell’equatore celeste e si è detto che esso è perpendicolare all’asse celeste.
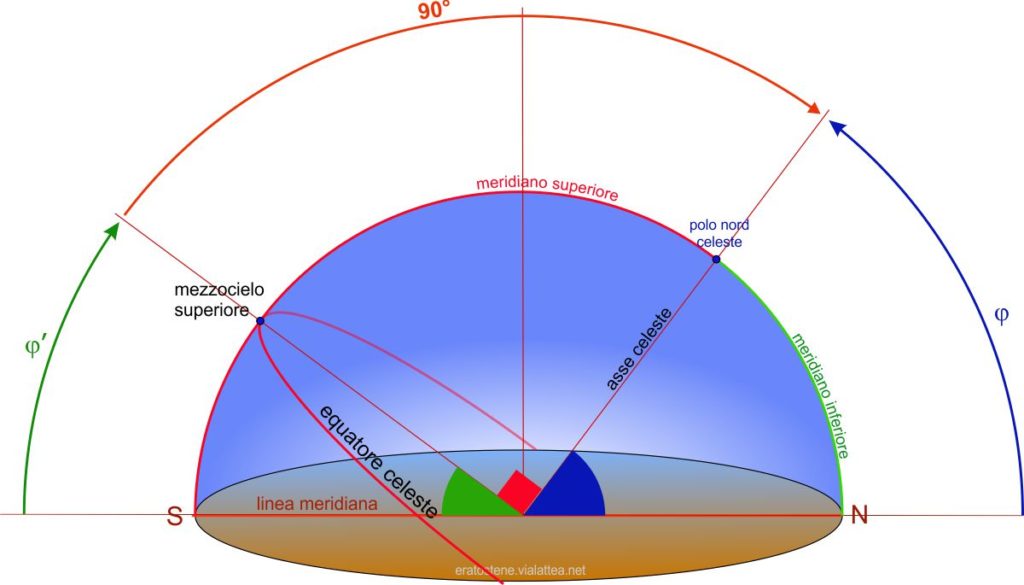
Di conseguenza, l’altezza del mezzocielo superiore $\varphi’$ è un angolo complementare all’altezza del polo $\varphi$ e perciò, conoscendo l’una si calcola facilmente l’altra:
$$\varphi’ = 90° – \varphi$$
Questa relazione tra altezza del polo e altezza del mezzocielo non è solo una curiosità geometrica: con un ingegnoso stratagemma, essa ci permetterà di determinare i giorni degli equinozi.

Date queste stesse relazioni, l’altezza del polo $\varphi$ è misurabile anche come distanza zenitale del mezzocielo, mentre l’altezza del mezzocielo si può ottenere misurando la distanza zenitale del polo elevato.
La distanza zenitale del mezzocielo superiore $\varphi$ è nota con il nome latitudine astronomica mentre il suo angolo complementare $\varphi’$ è chiamato colatitudine. La variazione della latitudine astronomica misurata da varie località metterà in crisi l’idea ingenua che la Terra è piatta e porterà alla determinazione della posizione geografica dell’osservatore.
Indice
< Gli archi visibili delle stelle
> La ricerca degli equinozi

