- Misurare la latitudine con l’altezza del Sole
- Metodo delle stelle circumpolari
- Altezza della stella Polare
a cura di Lucia Corbo e Nicola Scarpel
Misurando l’altezza del Sole al mezzogiorno vero è possibile determinare facilmente la latitudine astronomica ($\varphi$).
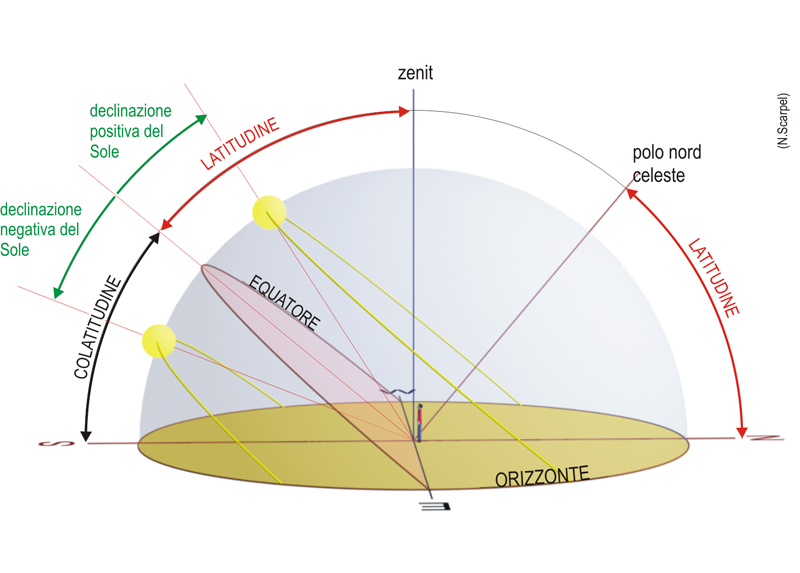
L’altezza del Sole $h$, la sua declinazione $\delta$, e la colatitudine $c$ (complemento a $90^\circ$ della latitudine) sono legati dalla semplice relazione:
$$h = c + \delta$$
Conoscendo due di questi angoli è immediato ricavare il terzo. Per il nostro scopo, conoscendo la declinazione del Sole $\delta$ e misurando la sua altezza $h$, si può determinare la latitudine astronomica del luogo $\varphi$:
$$c= h – \delta$$
$$\varphi = 90° – c$$
perciò:
$$\varphi = 90^\circ – h + \delta$$
I momenti più significativi per eseguire le misurazioni sono quelli in cui la declinazione è nota: i solstizi e gli equinozi. Al solstizio di dicembre il Sole, al mezzogiorno solare vero, raggiunge la sua minima altezza sull’orizzonte (corrispondente alla declinazione: $-23^\circ27’$). Al contrario, nel solstizio di giugno il Sole raggiunge la massima altezza (declinazione $+23^\circ27’$). Nel caso degli equinozi, il Sole si trova all’equatore celeste e la declinazione è $0^\circ$. In quest’ultimo caso la latitudine si ottiene con una semplice sottrazione:
$\varphi = 90^\circ – h$
La determinazione della latitudine può essere eseguita comunque in qualunque giorno dell’anno, basta conoscere la declinazione del Sole in quel giorno. Si può consultare una tavola di effemeridi oppure, più semplicemente, usare il nostro calcolatore delle declinazioni solari.
In ogni caso, la misura deve essere eseguita nell’istante del mezziogiorno vero cioè del transito del Sole al meridiano, il quale non corrisponde al mezzogiorno dei nostri orologi. Se si è disegnata una linea meridiana, tale istante si identifica empiricamente con il momento in cui l’ombra di uno gnomone verticale si allinea ad essa. Più semplicemente, si può utilizzare questo modulo che calcola il momento del mezzogiorno in base alla data e alla longitudine del luogo.

