Longitudine e case dello zodiaco
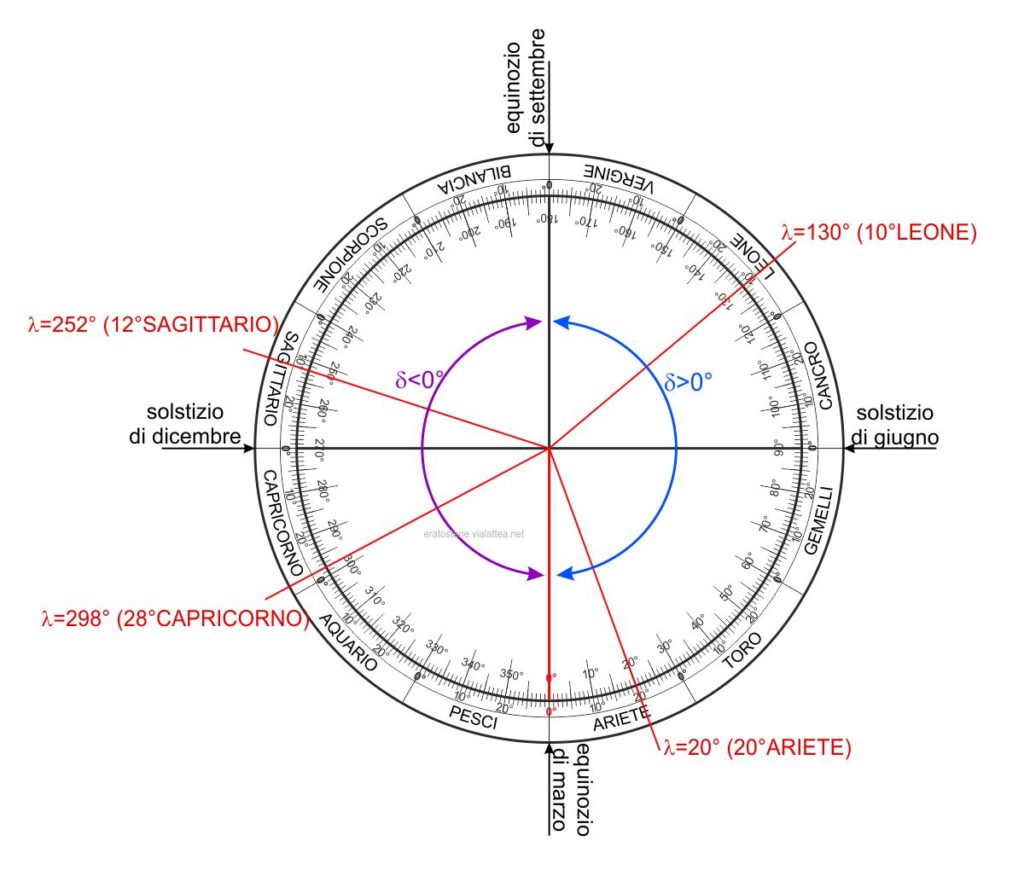
Tornando un po’ indietro nel tempo, come spesso facciamo in queste pagine, scopriamo che il conteggio tradizionale della longitudine era piuttosto diverso da quella attuale. L’eclittica era suddivisa in dodici settori di $30^\circ$ ciascuno: le case dello zodiaco. Ogni casa porta il nome della costellazione che, due millenni fa, era contenuta in quel settore di cielo. La prima casa è quella dell’Ariete il cui punto zero, chiamato primo punto dell’Ariete o punto vernale, coincide con lo zero della scala moderna delle longitudini. Il trentesimo grado dell’Ariete coincide con il primo punto della casa successiva, quella del Toro e così via. Questo sistema di suddivisione corrisponde anche ad una modalità di conteggio della longitudine eclittica; ad esempio, gli attuali $130^\circ$ di longitudine corrispondono ai $10^\circ$ del Leone, gli attuali $252^\circ$ ai $12^\circ$ del Sagittario, eccetera.
E’ una modalità di conteggio che ha alcuni vantaggi rispetto alla semplice scala moderna delle longitudini. Conoscendo l’ordine delle case zodiacali, la posizione del Sole all’interno di una certa casa ci informa con immediatezza la situazione calendariale rispetto ai solstizi e agli equinozi e quindi alle stagioni astronomiche. Ad esempio, i $10^\circ$ del Leone ci dicono che è piena estate boreale perché il Sole è a $40^\circ$ dal solstizio di giugno e gli mancano $50^\circ$ da percorrere per arrivare all’equinozio di settembre. Il settore destro dello schema rappresenta il periodo dell’anno in cui la declinazione del Sole è positiva (primavera ed estate boreali), la parte sinistra indica il periodo di declinazione negativa (autunno ed inverno boreali).
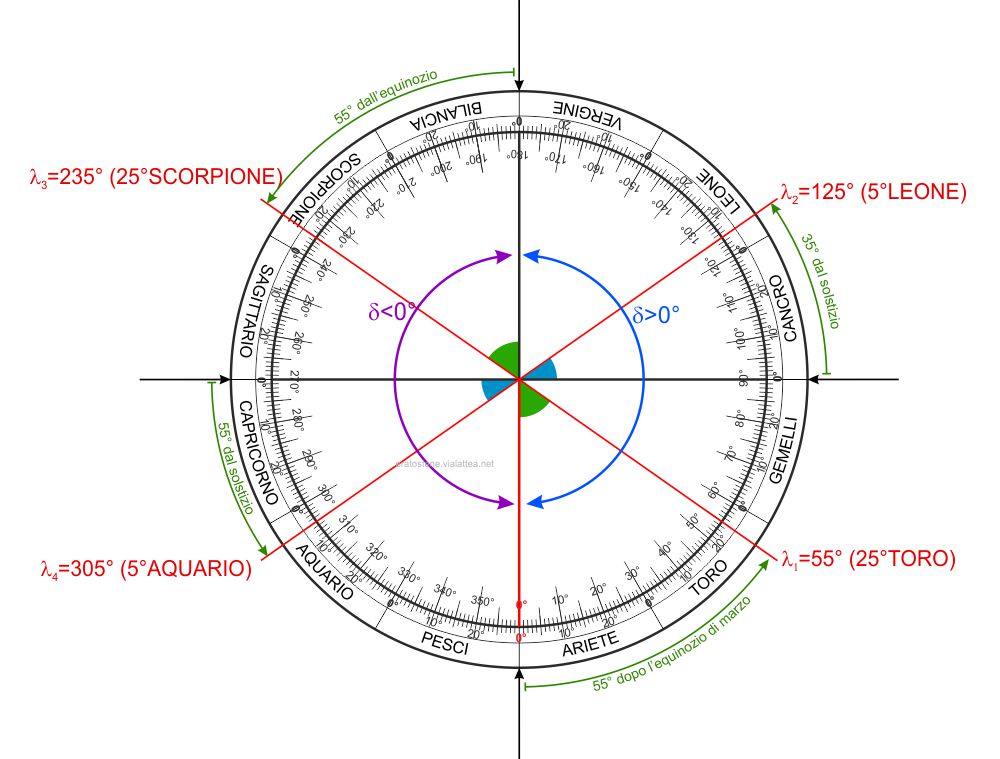
Per ritornare al nostro quadrante dei seni, osserviamo con cura queste quattro longitudini di esempio. Si scoprirà che la loro simmetria corrisponde matematicamente ad un’uguaglianza dei seni, se considerati nel loro valore assoluto:
$$\sin{55^\circ}=\sin{125^\circ}=-\sin{235^\circ}=-\sin{305^\circ}$$
Fatta questa considerazione, possiamio costruire un metodo per “comprimere” i $360^\circ$ di longitudine all’interno del settore di soli $90^\circ$ del nostro quadrante.

