L’arco dei seni e l’arco dei coseni
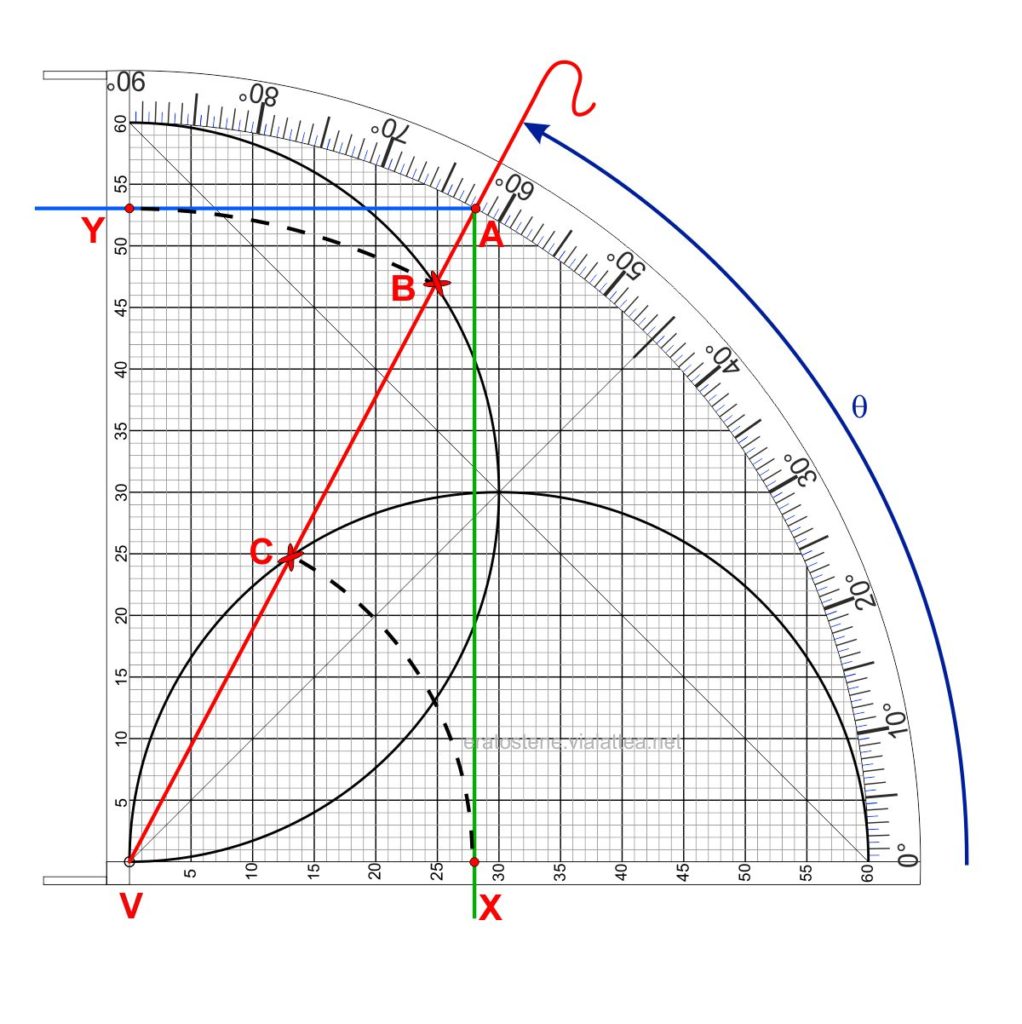
Vediamo ora il significato dell’arco dei seni e dell’arco dei coseni, cioè delle due semicirconferenze che hanno i loro diametri sulle scale.
Se il cordino è posizionato su $62^\circ$ (punto $A$), la sua intersezione con l’arco dei seni è il punto $B$. Quest’ultimo fornisce una distanza $VB$ che è uguale al valore del seno di $62^\circ$. Lo si può verificare puntando il compasso in $V$ e tracciando l’arco $BY$. Il punto $Y$ ha la stessa ordinata del punto $A$ e corrisponde al valore $\sin{62^\circ}=\frac{53}{60}$. Il cursore sistemato sul cordino nel punto $B$ serve a memorizzare il seno dell’angolo e acquista perciò la funzione della “memoria di massa” del nostro computer analogico.
In modo analogo, l’intersezione del cordino con l’arco dei coseni fornisce la distanza $VC=VX=\cos{62^\circ}=\frac{28}{60}$, che è anche l’ascissa del punto $A$.
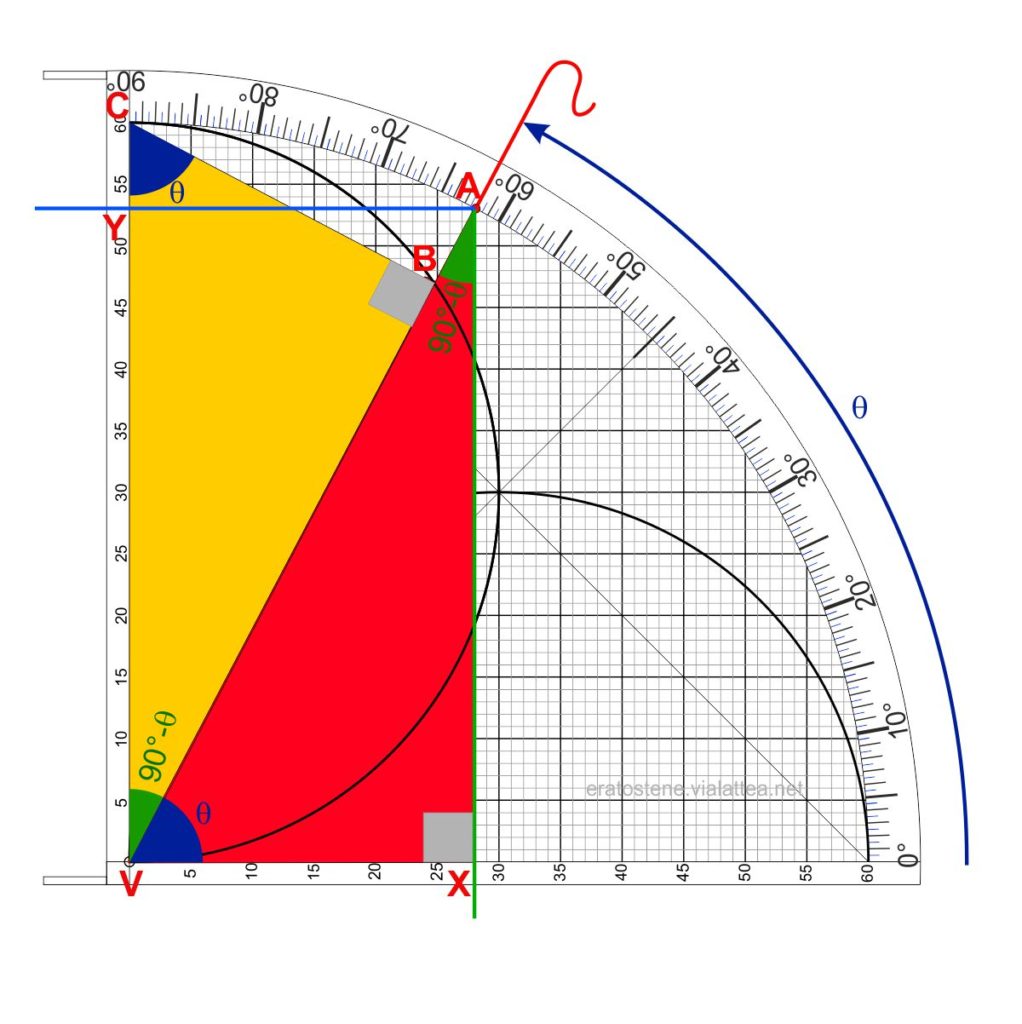
Come mai gli archi dei seni e dei coseni hanno questa proprietà? Ricordiamo una proprietà dei triangoli rettangoli: un triangolo rettangolo inscritto in una circonferenza ha l’ipotenusa come diametro.
Nella figura qui a fianco vediamo che il triangolo $CVB$ è necessariamente rettangolo perché è inscritto nell’arco dei seni ed ha l’ipotenusa $CV$ come suo diametro.
Si rappresenta inoltre il triangolo $AVX$ formato dall’ipotenusa $AV$ che si trova lungo il cordino e dai cateti $AX$ e $VX$ che sono rispettivamente l’ordinata e l’ascissa del punto $A$.
E’ facile dimostrare che questi due triangoli sono congruenti (l’ipotenusa di entrambi è uguale al raggio del quadrante e i loro angoli sono rispettivamente congruenti).
In conclusione, la distanza $VB$ “memorizzata” dal cursore è uguale all’ordinata $VY$ del punto $A$ cioè al seno dell’angolo $\theta$.
Una dimostrazione analoga riguarda l’arco dei coseni.

