Il rapporto tra due funzioni trigonometriche
Fino ad ora abbiamo visto che il prodotto tra seni e coseni si risolve con un unico metodo a patto di trasformare tutti i coseni in seni per mezzo della lettura “rovescia” degli angoli. E’ un metodo che sembra complesso a prima vista ma, se viene ripetuto alcune volte diventa semplice. Gli unici calcoli da fare sono eventualmente delle sottrazioni da $90°$, tutto il resto è fatto di azioni meccaniche.
Vediamo ora di trovare il valore dell’angolo $\theta$ dalla seguente equazione:
$$\sin{\theta}= \frac{\sin{\alpha}}{\sin{\beta}}$$
con $\alpha=21^\circ\!,\!5$ e $\beta=28^\circ$.
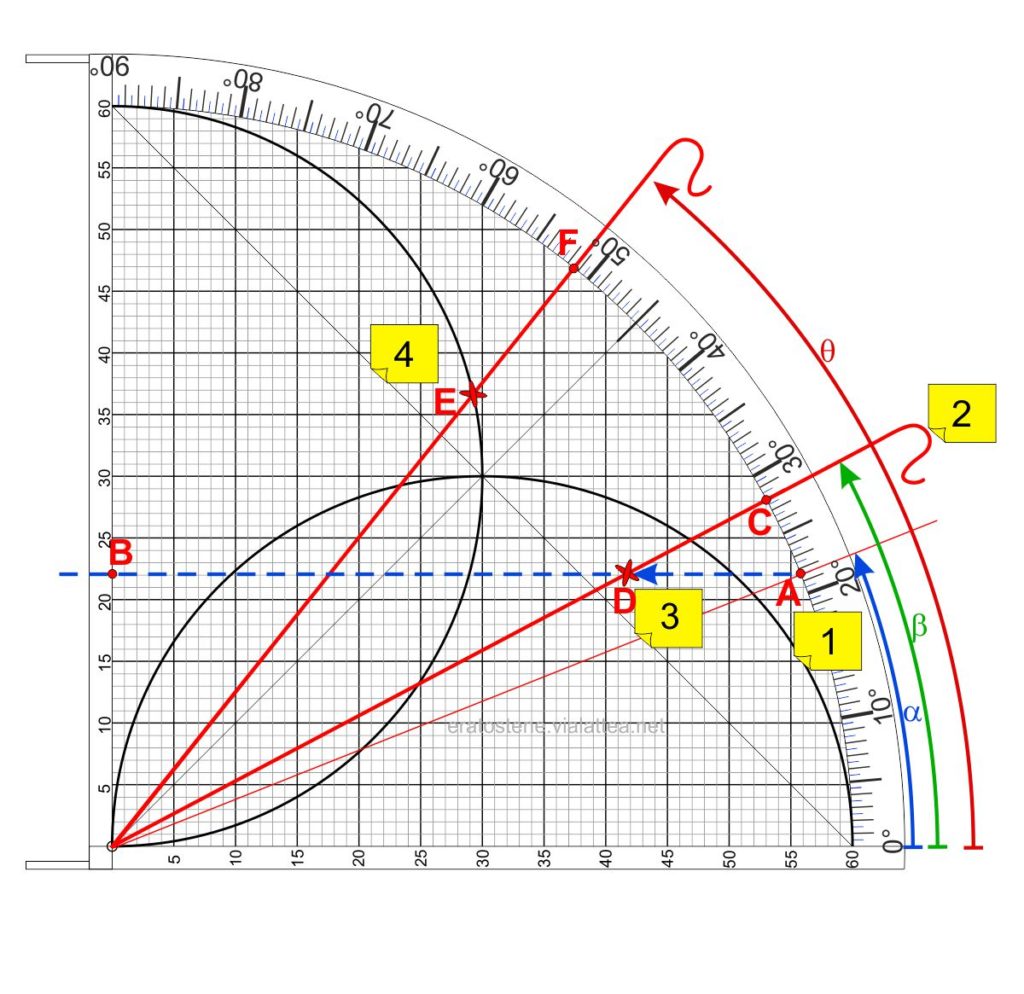
In presenza di un rapporto tra funzioni trigonometriche si può procedere a ritroso, con un meccanismo inverso rispetto a quello usato nella moltiplicazione. Seguiamolo passo passo:
- Si traccia idealmente l’orizzontale $AB$ la cui ordinata è uguale a $\sin21^\circ\!,\!5$.
- Si posiziona il cordino nel punto $C$ dell’arco degli angoli sul valore $\beta=28^\circ$.
- Si fa scorrere il cursore lungo il cordino fino al punto $D$ che è la sua intersezione con la retta $AB$ trovata prima.
- Si sposta il cordino in modo tale che il suo cursore ruoti fino al punto $E$ di intersezione con l’arco dei seni. Quindi si legge il valore dell’angolo $\theta=51^\circ\!,\!5$ nel punto $F$.

