Trasformare i coseni in seni
Vediamo ora di risolvere la seguente equazione nella quale compaiono due coseni:
$$\cos{\theta}=\sin{\alpha}\cdot\cos{\beta}$$
Poniamo come esempio $\alpha=53^\circ$ e $\beta=60^\circ$. Si procederà con un metodo molto simile al precedente, ma semplificheremo le cose trasformando tutti i coseni in seni sapendo che il coseno di un angolo è uguale al seno del suo complementare.
Vediamo come.
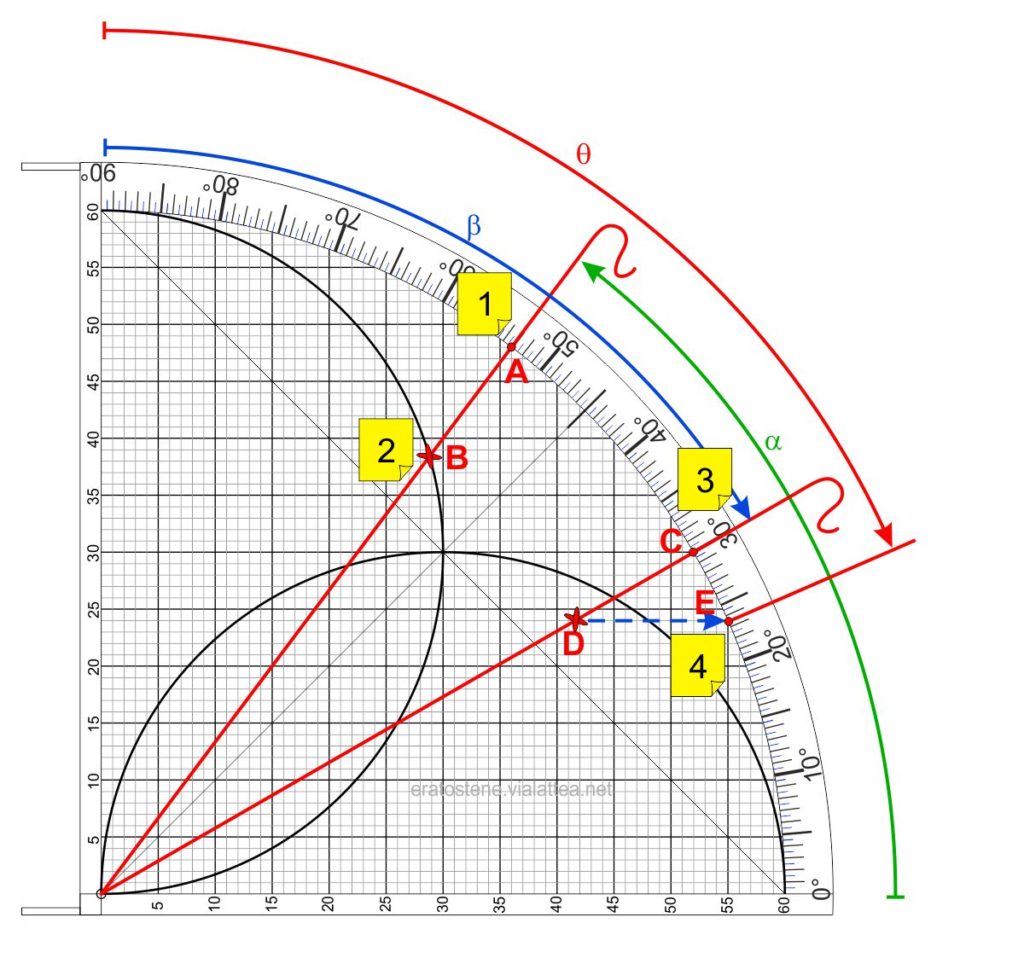
- Portiamo il cordino nel punto $A$ dell’arco degli angoli in modo che indichi $53^\circ$.
- Spostiamo il cursore fino a raggiungere il punto $B$ di intersezione con l’arco dei seni.
- Ora dobbiamo operare con $\cos{\beta}$ che trasformiamo in $\sin{(90^\circ-\beta)}$ e quindi spostiamo il cordino sul punto $C$ che indica $90^\circ-60^\circ=30^\circ$
- Con quest’ultimo spostamento il cursore $B$ ruota in posizione $D$. La retta orizzontale che passa per $D$ ci porta nel punto $E$ dove leggiamo $23^\circ\!,\!5$. Questo sarebbe il valore di $\theta$ se il problema avesse richiesto $\sin{\theta}$. Noi invece dobbiamo leggere il valore di $\theta$ “al rovescio”. Il risultato è:
$$\theta = 90^\circ-23^\circ\!,\!5=66^\circ\!,\!5$$
Alcuni antichi quadranti dei seni presentano solo la griglia orizzontale. Probabilmente la funzione seno era, in origine, l’unica utilizzata sul quadrante. D’altra parte la trasformazione dei coseni in seni semplifica, generando meno confusione, ed aiuta a rendere automatica l’operazione manuale del calcolo.

