Funzioni di base: trovare il seno e il coseno di un angolo
Prima di procedere è bene chiarirsi sui termini usati. Se ruotiamo il quadrante in modo da orientare verticalmente la scala dei seni (quella con i traguardi), tutte le considerazioni che faremo risulteranno più comprensibili per due ragioni:
- l’asse dei seni e l’asse dei coseni diventano rispettivamente gli assi $Y$ e $X$ di un piano cartesiano orientato nel modo abituale.
- l’arco degli angoli può essere pensato come il primo settore di un cerchio trigonometrico, anch’esso orientato nel modo abituale, con la scala dei gradi che origina sull’asse $X$ e che cresce in senso antiorario.
Perciò quando fissiamo un punto $A$ qualsiasi sulla griglia, con l’espressione ascissa di A si intende il valore che si trova sulla scala dei coseni all’intersezione con la retta verticale della griglia che passa per il punto $A$. Analogamente, l’ordinata di A è il valore che si trova sulla scala dei seni all’intersezione della retta orizzontale della griglia che passa per il punto $A$. In questo caso l’ascissa di $A$ vale $\frac{15}{60}=0,25$ e la sua ordinata è $\frac{30}{60}=0,5$.
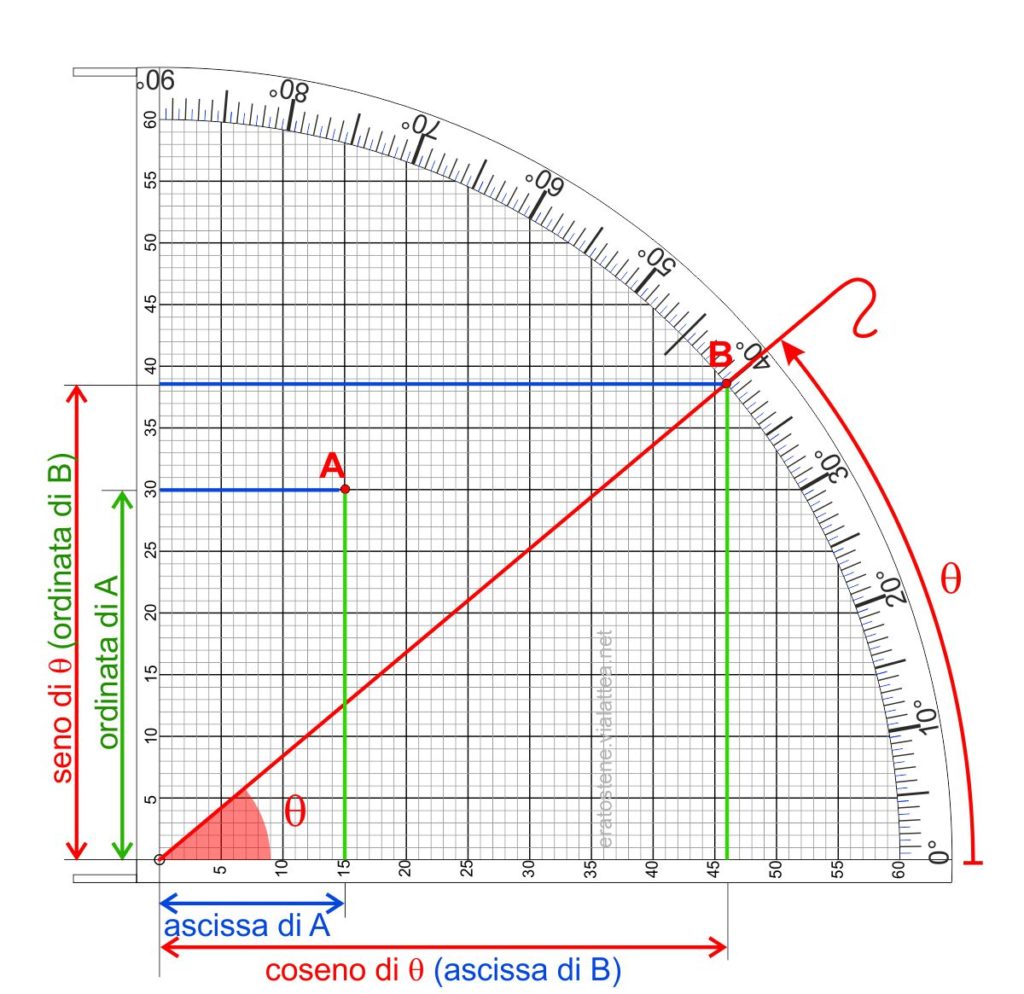
Le coordinate dei punti che si trovano sull’arco degli angoli, come ad esempio il punto $B$, hanno una proprietà speciale perché ci permettono di trovare immediatamente il seno e il coseno di un angolo. Il punto $B$ del nostro esempio si trova sui $40^\circ$ dell’arco degli angoli. Il cordino che passa sul punto $B$ apre un angolo $\theta=40^\circ$ rispetto alla scala dei coseni. Di conseguenza, l’ordinata del punto $B$ è uguale al seno di $\theta$ espresso in sessantesimi (in questo caso $\sin\theta=\frac{38,5}{60}$). Analogamente, l’ascissa di $B$ è uguale al coseno di $\theta$ espresso in sessantesimi (in questo caso $\cos{\theta}=\frac{46}{60}$.
In gran parte dei casi, come vedremo, non sarà necessario eseguire le divisioni per trovare i valori decimali di seno e coseno compresi tra $0$ e $1$ ai quali siamo abituati.

