Trovare la tangente di un rapporto
Molto più intuitivo è risolvere la seguente equazione:
$$\tan{\theta}= \frac{\sin{\alpha}}{\sin{\beta}}$$
con i seguenti valori: $\alpha=53^\circ$ e $\beta=21^\circ\!,\!5$.
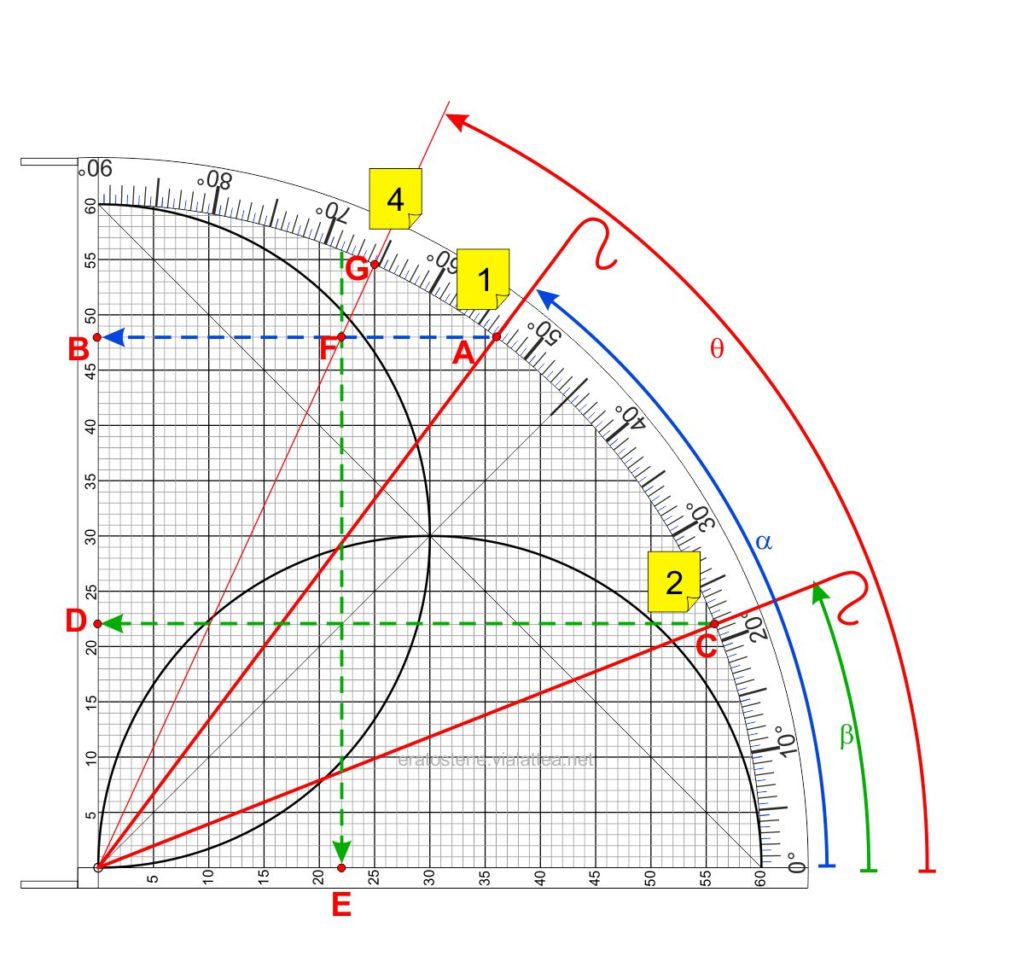
Sappiamo infatti che la tangente di un angolo è uguale al rapporto tra il seno e il coseno. Possiamo così imitare sul quadrante il rapporto tra i cateti di un triangolo rettangolo. Ecco i passi da eseguire:
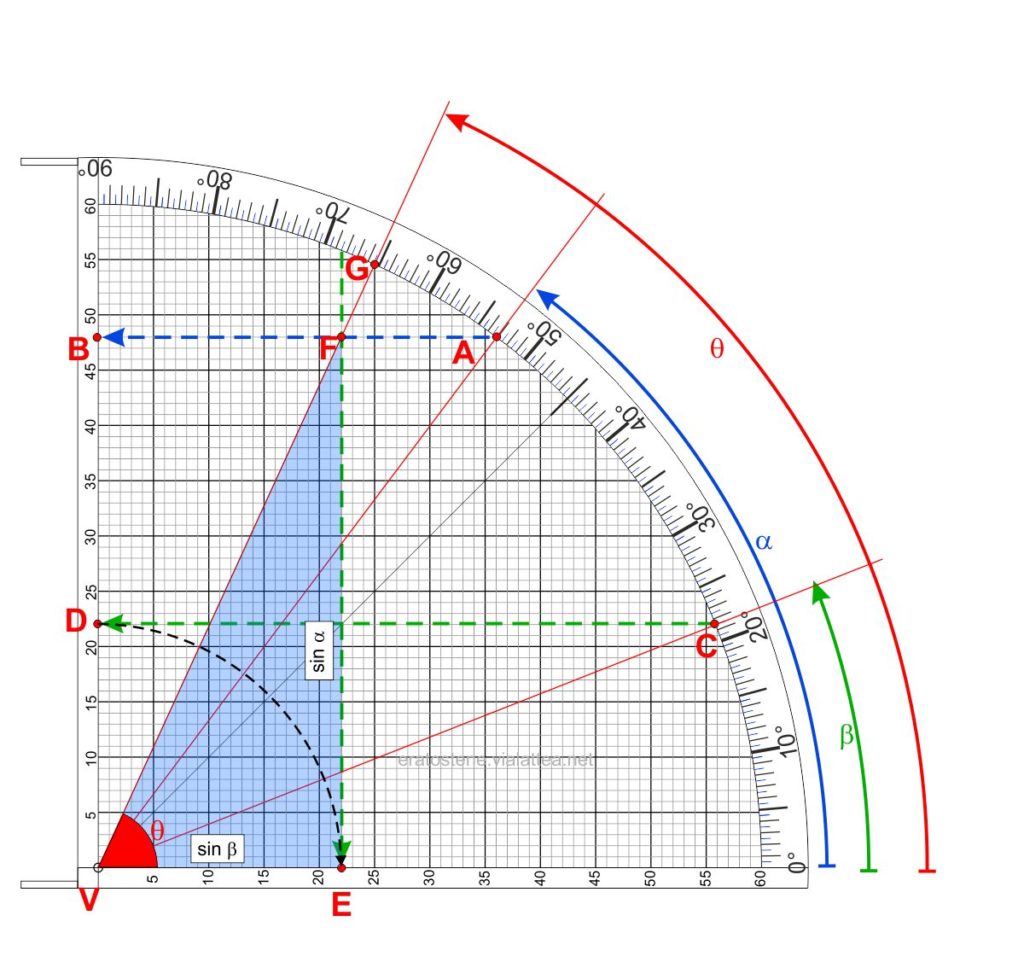
- Portiamo il cordino in corrispondenza del punto $A$ dell’arco degli angoli che indica il valore dell’angolo $\alpha$. Troviamo l’ordinata di questo punto leggendo in $B$ il valore $45/60$ che dobbiamo memorizzare.
- Portiamo il cordino nel punto $C$ corrispondente al valore dell’angolo $\beta$ e leggiamo la sua ordinata nel punto $D$ che vale $22/60$.
- Immaginiamo di tracciare una retta orizzontale che ha ordinata $22/60$ uguale all’ordinata di $C$. Questa retta passerà per il punto $E$.
- L’orizzontale che passa per $B$ e la verticale che passa per $E$ si intersecano nel punto $F$. L’angolo $\theta$ si ottiene facendo passare il cordino per il punto $F$. Il suo valore si legge nell’arco degli angoli al corrispondente punto $G$ ($65^\circ\!,\!5$).
Può capitare facilmente che l’intersezione tra ascissa e ordinata non si trovi all’interno del quadrante: in questo caso basta dimezzare una o due volte i valori di ascissa e ordinata. Si perde in precisione ma si raggiunge comunque l’obiettivo.
In sostanza, con questa tecnica si costruisce il triangolo rettangolo $FVE$ i cui cateti misurano $\sin{\alpha}$ e $\sin{\beta}$. L’angolo alla base $\theta$ è tale per cui:
$$tan{\theta} = \frac{\sin{\alpha}}{\sin{\beta}}$$