Indice | >Come si muove la sfera celeste?
Considero un buon inizio quello di fingere di non sapere nulla e di affrontare l’osservazione del cielo e del moto degli astri con lo stesso atteggiamento che avrebbe un bambino o un astronomo di una remota antichità. Le considerazioni a cui si giunge con questa modalità “primitiva” sono sicuramente molto semplici e ingenue ma contengono quei modelli geometrici che nel corso dei millenni hanno favorito lo sviluppo dell’astronomia, della matematica e delle scienze in generale. Esaminiamo alcuni aspetti di questa meravigliosa semplificazione.
- Le superfici delle pianure che attraversiamo e dei mari che solchiamo ci suggeriscono l’idea che la Terra sia un oggetto piatto, probabilmente circolare, una specie di disco di spessore ignoto sul quale viviamo. Siamo troppo piccoli rispetto al nostro pianeta per accorgerci della sua sfericità. Un batterio che vive sulla superficie di un pallone da calcio sarebbe convinto di essere appoggiato su una superficie piana. Sopra di noi c’è la cupola azzurra della volta celeste. Sulla sua superficie sono cosparse le stelle. Basta osservarle per qualche ora della notte e nel corso di alcune notti successive per capire che molte di esse scompaiono a occidente per ricomparire a oriente: la volta celeste si estende anche sotto la Terra. Quella che vediamo e che chiamiamo volta è solo la metà visibile di una sfera che ci circonda: la sfera celeste.
- Le stelle sembrano essere collocate sulla superficie della sfera celeste mantenendo posizioni reciproche costanti che ci permettono di disegnare una “geografia” di costellazioni dalle forme apparentemente immutabili e quindi sempre riconoscibili.
- Non si conosce la distanza delle stelle. Sono sicuramente molto lontane, molto più lontane degli oggetti che si vedono al limite dell’orizzonte. Il raggio della sfera celeste non è misurabile. La nostra istintiva capacità di valutazione delle distanze fallisce quando si osservano le stelle.
- L’idea della sfera ci viene suggerita dal particolare moto delle stelle: esse “ruotano” attorno a noi, solidali tra loro. Ciascuna stella percorre sempre lo stesso circolo, e lo completa in un giorno. Gli astri sembrano perciò incastonati sulla superficie interna di una sfera che potrebbe essere pensata anche come un oggetto “rigido” che ruotaci attorno a noi.
- Alcuni astri, come il Sole, la Luna e i pianeti, metteranno un po’ in crisi questa idea della sfera rigida. Essi infatti possiedono un certo grado di libertà dalla sfera e, pur essendo “trascinati” da essa nel suo moto diurno, si muovono rispetto alle stelle, più o meno velocemente. Fin dall’antichità si distinguono due categorie principali di corpi celesti: le stelle fisse e gli “oggetti vaganti”.
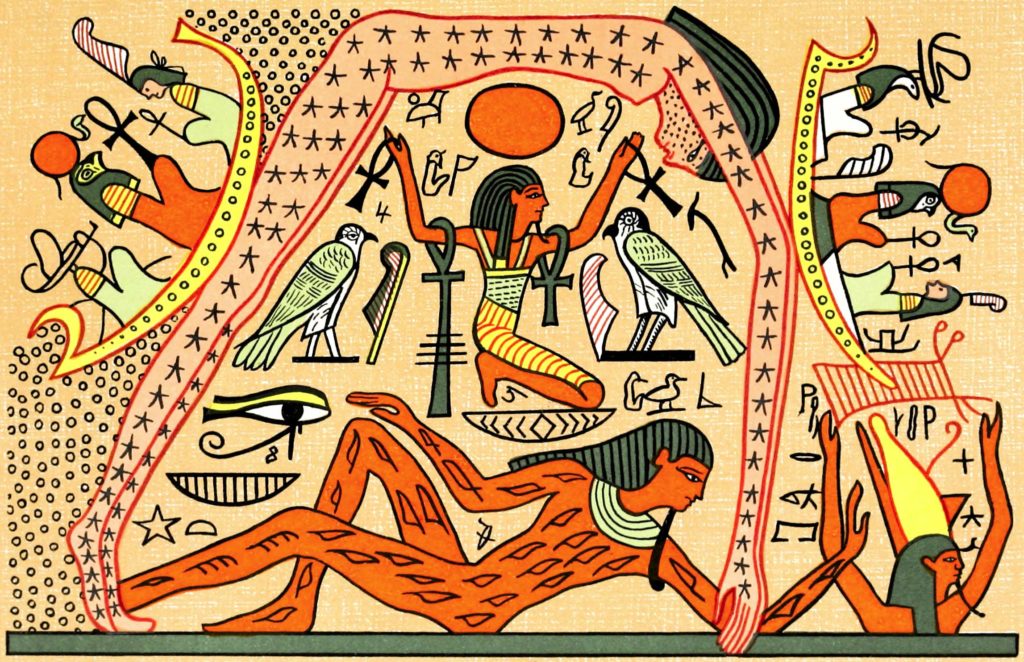
Nut, dea egiziana del cielo, era rappresentata come un corpo femminile nudo, cosparso di stelle, con i piedi e le mani che toccano il suolo, quest’ultimo personificato dal dio Geb. Nut è sostenuta da Shu, dio dell’aria (immagine da wikimedia)
Si può sintetizzare la forma dell’universo primitivo per mezzo di due oggetti geometrici sostanzialmente semplici: una sfera e un piano.
Il primo tentativo di applicare la matematica all’interpretazione del cielo consiste nel trovare un modo per descrivere la posizione degli astri per mezzo di un sistema di misura. Data la distanza indefinibile degli astri, ci rimane solo la possibilità di misurare le loro direzioni per mezzo di angoli.
Per misurare la distanza angolare tra due astri basta utilizzare un semplice strumento come la balestriglia. Per misurare invece la direzione di un astro rispetto a qualche riferimento fisico del nostro orizzonte la questione diventa un po’ più complessa. Se scegliessimo una montagna, un albero o un edificio, le misure sarebbero valide soltanto per il luogo specifico dal quale si osserva (vedi parallasse).

Archipendolo, uno strumento per controllare l’orizzontalità.
Il campo gravitazionale terrestre ci viene in aiuto: la verticalità e l’orizzontalità sono innanzitutto sensazioni propriocettive, ma sono anche fenomeni materializzabili dal filo a piombo e dalla superficie di un liquido a riposo. Il nostro cervello le può tradurre facilmente in concetti astratti, geometrici. L’angolo compreso tra loro è l’angolo retto, il più “istintivo” che si possa concepire. E’ un angolo facilmente riproducibile essendo esattamente la quarta parte del piano (*). Si possono costruire squadrette e strumenti di misura. Se si conosce la direzione verticale si può definire anche un piano orizzontale e viceversa. La retta verticale e il piano orizzontale possono essere utilizzati come riferimenti “standard” per la misura della direzione di un astro. In prima approssimazione essi sono indipendenti dal luogo di osservazione. Qualsiasi osservatore ha a disposizione una direzione verticale e un piano orizzontale, controllabili da strumenti, per le sue misurazioni delle direzioni degli astri.
Le esperienze che descriveremo richiederanno spesso il filo a piombo per controllare la verticalità e una livella, oppure un archipendolo, antenato più semplice della livella ma altrettanto preciso, per l’orizzontalità.
In base a questi semplici concetti si può già misurare l’altezza di un astro rispetto al piano dell’orizzonte. Ad esempio, l’altezza del Sole si ottiene misurando l’ombra proiettata da uno gnomone, un bastone verticale piantato su una superficie orizzontale. Il metkhet, antico strumento egiziano che consiste essenzialmente in un filo a piombo usato per traguardare gli astri, ci permette di misurare l’altezza delle stelle.

Se si desidera annotare la posizione di un astro per comunicarla ad un altro osservatore o per confrontarla con successive osservazioni, la sola misura dell’altezza, che è un angolo “verticale”, non è sufficiente. E’ necessario anche un angolo “orizzontale” che ci permetta di ritrovare la direzione della stella rispetto ad un qualche punto di riferimento “fisso” posto all’orizzonte. Quest’ultima misura è chiamata azimut. La scelta di un riferimento “standard” dal quale partire per misurare l’azimut non è un’operazione semplice come quella della scelta del piano orizzontale per misurare l’altezza. Non si può certo scegliere una torre e nemmeno la cima di una montagna all’orizzonte. E’ necessario trovare una direzione legata ad una caratteristica costante del moto della sfera celeste e del suo assetto rispetto all’osservatore. La ricerca dei punti cardinali è un’operazione astronomica di una certa complessità, che sarà affrontata nelle prossime pagine, e che rappresenta proprio la ricerca di un orientamento sulla Terra rispetto alla posizione delle stelle. Attualmente il punto cardinale nord è il riferimento per la misura dell’azimut.
Altezza e azimut sono le coordinate di un sistema di riferimento fondamentale in astronomia: il sistema altazimutale, e sono le prime che utilizzeremo.
Riassumendo, l’immagine ingenua del mondo offre alcuni elementi geometrici che sono alla base di qualsiasi tentativo di misurazione astronomica: il piano orizzontale della Terra, la retta verticale perpendicolare ad essa e la sfera celeste indefinitamente grande e in perenne rotazione.
(*) E’ interessante notare che l’angolo retto è la quarta parte esatta del piano. Altri modi semplici di divisione del piano sono in 3 e in 5 parti uguali. L’unità di misura degli angoli più antica è il grado sessagesimale ottenuto da una divisione del piano in 360 parti uguali. Il numero 360 è particolarmente interessante per vari motivi: i suoi fattori primi sono soltanto il 2, il 3 e il 5 ma possiede ben 22 divisori oltre a 1 e se stesso (2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 40, 45, 60, 72, 90, 120 e 180). E’ uguale a 6 volte 60. Il 60 è la base del sistema di numerazione sessagesimale, utilizzato al giorno d’oggi nelle misure di tempo e di angoli e inventato dai Sumeri almeno 5000 anni fa.

