- Il quadrato delle ombre
- Il quadrante dei seni
- La balestriglia
- Archipendolo
- Quadranti fissi e mobili
- Il merkhet e la posizione delle stelle
- Foro gnomonico e camera oscura
- Calcolatore grafico della declinazione solare

Archipenzolo in ottone del secolo XVII (Museo Galileo).
Si potrebbe dire che l’archipendolo o archipezolo è l’antenato della livella. Permetteva non solo di controllare l’orizzontalità ma anche l’inclinazione di una superficie ed era usato nell’edilizia e in campo militare per controllare l’inclinazione dei cannoni. Ha la forma di un triangolo rettangolo isoscele. E’ costituito da due gambe perpendicolari tra loro e di uguale lunghezza. Un’asta graduata unisce le due gambe formando con esse angoli di $45^\circ$. I piedi delle gambe, paralleli all’asta graduata, servono per appoggiare lo strumento su una superficie. Il filo a piombo, agganciato al vertice, permette di controllare l’inclinazione del piano su cui si appoggia lo strumento, leggendo il valore sul punto dove il filo attraversa l’asta graduata. Quando la direzione del filo coincide con l’asse di simmetria dello strumento, il piano è orizzontale.
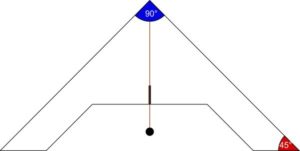
Rispetto alla livella a bolla, strumento tecnicamente più sofisticato, l’archipendolo è semplice da costruire e forse più preciso. Se si intende usare l’archipendolo solo per controllare l’orizzontalità di un piano, basta tracciare un’unica tacca nel punto medio dell’asta.
Per usarlo come inclinometro si può aggiungere una scala dei gradi. Se $i$ è l’inclinazione dello strumento rispetto all’orizzontalità e $r$ la distanza tra il vertice e il punto medio dell’asta, la tacca corrispondente all’inclinazione $i$ va segnata ad una distanza $d$ dal punto medio dell’asta, calcolabile con la formula: $d=r\cdot\tan{i}$.
L’archipendolo può essere costruito su legno compensato usando una squadretta a $45^\circ$ per tracciarne il contorno.

