I costruttori di orologi solari si trovavano spesso di fronte al problema di mettere in relazione le date del calendario con la declinazione del Sole. Un esempio è descritto in queste pagine nella costruzione dell’anello equinoziale e un altro esempio nell’analemma di Vitruvio. In sostanza, il problema si riduce ad una trasformazione di coordinate eclittiche in coordinate equatoriali e, in particolare, alla relazione matematica tra la longitudine dei punti dell’eclittica e la loro declinazione, dato che il Sole percorre l’eclittica. Il problema si può risolvere utilizzando una formula relativamente semplice:
$$\sin\delta=\sin\lambda\cdot\sin\epsilon$$
dove $\delta$ è la decinazione, $\lambda$ la longitudine eclittica e $\epsilon$ l’obliquità dell’eclittica che attualmente vale $\text{23,4}^\circ$ (per approfondire il significato matematico di questa formula, vedi coordinate equatoriali dei punti dell’eclittica).
Per evitare i calcoli o la consultazione di tavole, esiste anche un interessante metodo grafico per risolvere il problema, che descriviamo qui.
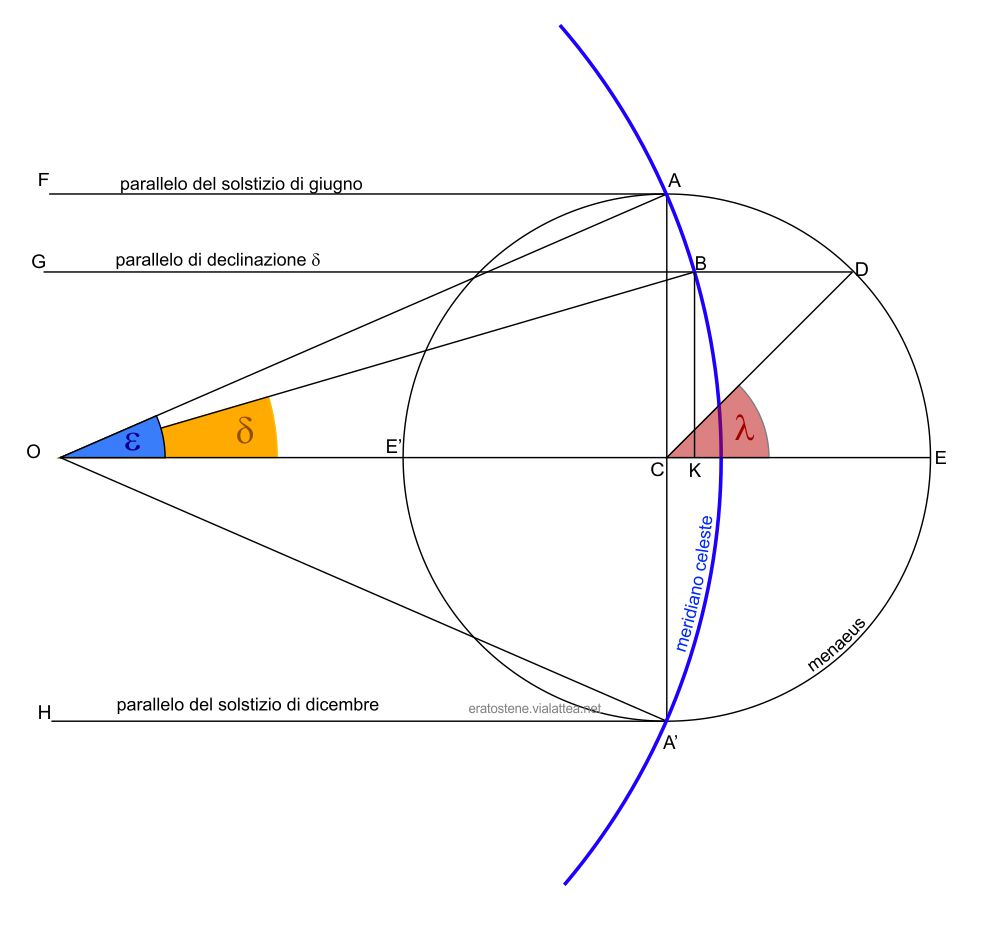
Si traccia un arco di cerchio che rappresenta il meridiano celeste, di centro $O$ e di raggio $OA$. Si traccia una semiretta $OE$ che rappresenta l’equatore celeste proiettato sul piano del meridiano. Dal centro $O$ si tracciano due raggi $OA$ e $OA’$ simmetrici rispetto all’equatore $OE$ e che formano con esso un angolo $\epsilon=\text{23,4}^\circ$. Si individuano così i due punti $A$ ed $A’$ sul meridiano che rappresentano i punti di declinazione massima e minima del Sole raggiunta ai solstizi.
Le due rette $AF$ e $A’H$, parallele all’equatore, che passano per i punti solstiziali $A$ e $A’$ rappresentano perciò i paralleli di massima e minima declinazione del Sole, cioè i circoli dei tropici proiettati sul piano meridiano.
Si traccia quindi una corda $AA’$ che diventa il diametro di un secondo cerchio di centro $C$, punto medio della corda. Su questo cerchio, che chiameremo menaeus (“mensile”), si può disporre una scala graduata dei $360^\circ$ di longitudine eclittica con lo zero nel punto $E$ e disposta in senso antiorario.
Aprendo un qualsiasi angolo come ad esempio $E\widehat{C}D$ di ampiezza uguale alla longitudine $\lambda$ desiderata, si identifica il corrispondente parallelo $DB$ il cui punto di intersezione $B$ con il cerchio meridiano ci permette di disegnare l’angolo $B\widehat{O}C$ la cui ampiezza è uguale alla corrispondende declinazione $\delta$ cercata.
Dimostriamo qui la relazione geometrica tra $\lambda$ e $\delta$, assumendo che il cerchio meridiano sia un cerchio trigonometrico di raggio unitario ($OA=1$). Ne deriva che il raggio del menaeus è:
$AC=\sin\epsilon$
Ricaviamo ora il segmento $BK$ sia in base al cerchio dell’analemma che in base al menaeus:
$BK=\sin\delta$
e
$BK=AC\cdot\sin\lambda=\sin\epsilon\cdot\sin\lambda$
infine, uguagliando le due precedenti si ottiene la formula che volevamo dimostrare:
$$\sin\delta=\sin\lambda\cdot\sin\epsilon$$
Seguendo la tradizione, il menaeus riporta la successione delle case zodiacali. Lo zero (primo punto di Ariete) si trova nel punto $E$ di intersezione con il piano equatoriale. La serie prosegue raggiungendo il punto solstiziale di giugno $A$ con il primo punto del Cancro $(\lambda=90^\circ)$, il primo punto della Bilancia $(\lambda=180^\circ)$ nel punto $E’$ nuovamente sull’equatore, ed infine il primo punto del Capricorno $(\lambda=270^\circ)$ nel punto $A’$ del solstizio di dicembre.
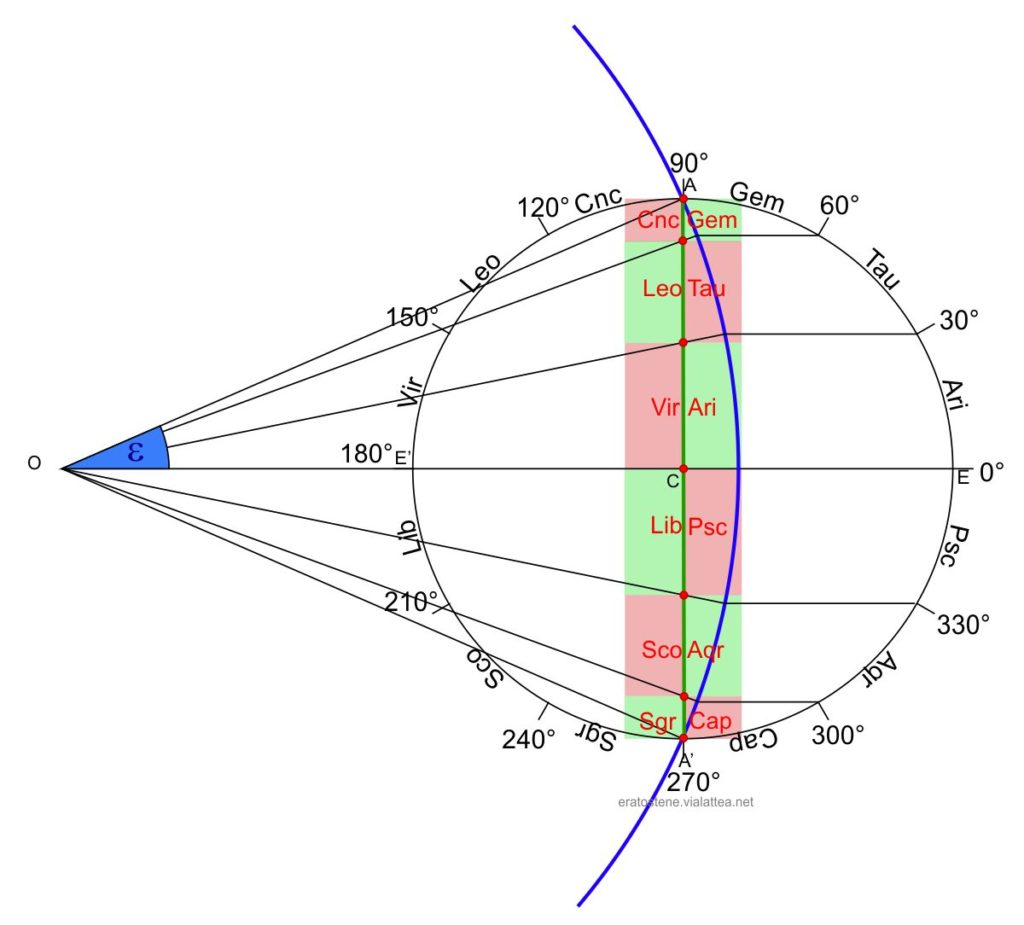
Le dodici case zodiacali possono essere proiettate facilmente sull’asse centrale delle declinazioni (il diametro del menaeus) ottenendo così una corrispondente scala di longitudini. La costruzione è particolarmente semplice per il fatto che le case sono di uguale ampiezza $(30^\circ$ ciascuna) e disposte in modo simmetrico rispetto a tale asse verticale.
Spesso, negli strumenti solari, la scala delle case zodiacali è accompagnata ai settori dei mesi, o sostituita da essi. Se vogliamo ad esempio costruire una suddivisione in mesi delle date di calendario, possiamo utilizzare la seguente tabella che fornisce per ogni primo giorno del mese la corrispondente longitudine, espressa anche in posizione sulle case zodiacali:
1 gen: δ=-23.02° λ=280,5° (10,5° Cap) 1 feb: δ=-17.16° λ=312,1° (12,1° Aqr) 1 mar: δ= -7.67° λ=340,4° (10,4° Psc) 1 apr: δ= +4.45° λ= 11,2° (11,2° Ari) 1 mag: δ=+15.01° λ= 40,6° (10,6° Tau) 1 giu: δ=+22.02° λ= 70,5° (10,5° Gem) 1 lug: δ=+23.12° λ= 99,2° ( 9,2° Cnc) 1 ago: δ=+18.07° λ=128,8° ( 8,8° Leo) 1 set: δ= +8.36° λ=158,6° ( 8,6° Vir) 1 ott: δ= -3.10° λ=187,8° ( 7,8° Lib) 1 nov: δ=-14.35° λ=218,5° ( 8,5° Sco) 1 dic: δ=-21.76° λ=248,8° ( 8,8° Sgr)
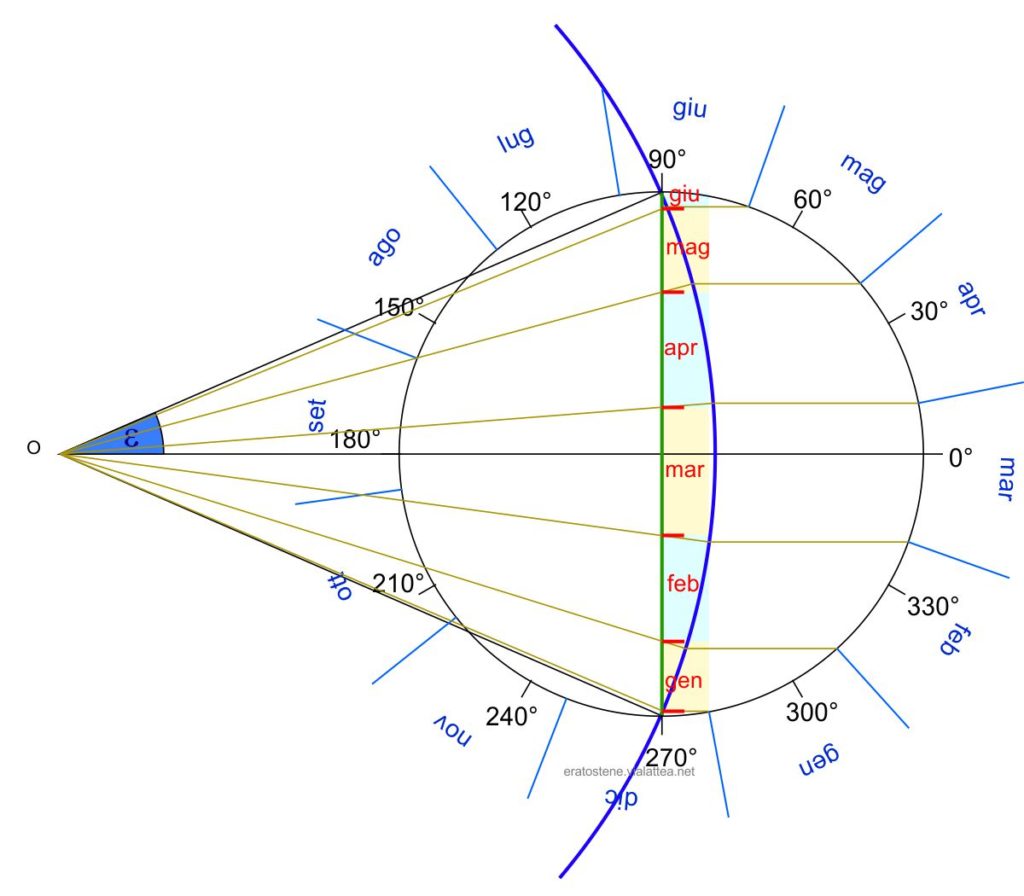
Disponendo così le posizioni delle date dei primi giorni di ogni mese lungo le case zodiacali si può affiancare all’asse delle declinazioni la scala calendariale. Rispetto alla costruzione precedente, qui si aggiunge una piccola complicazione dovuta alla non simmetria delle date rispetto all’asse delle declinazioni.
Per chiarezza, riportiamo prima soltanto le date del semicerchio destro del menaeus (quelle corrispondenti alle declinazioni crescenti). Notare che il metodo grafico è sempre lo stesso: si traccia la parallela all’equatore che parte dal punto di longitudine scelto e si giunge all’intersezione con il cerchio meridiano. Da questo punto si traccia un segmento che giunge al vertice $O$: l’intersezione di questo segmento con l’asse verticale indica il punto corrispondente alla longitudine scelta.
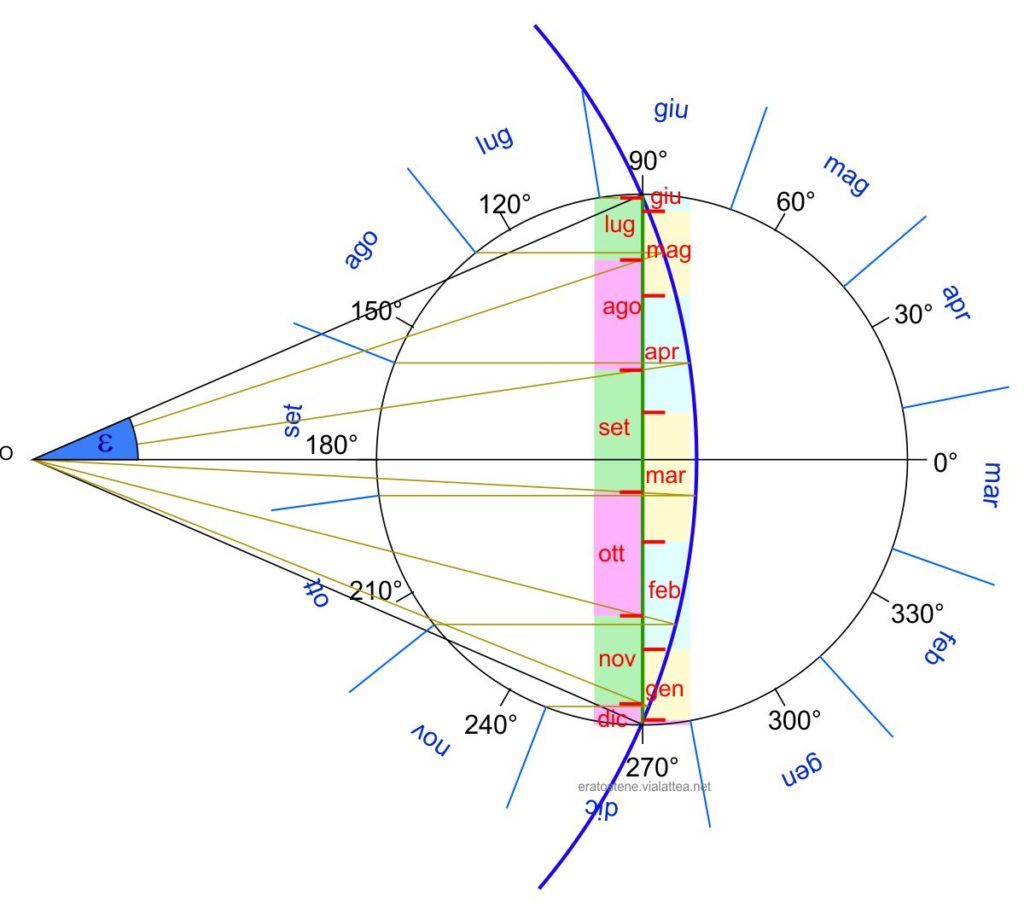
Completiamo ora il grafico con i settori dei mesi del semicerchio sinistro (declinazione decrescente). Il metodo di costruzione è analogo a quello descritto. Nel corso della costruzione si noteranno i casi particolari dei mesi di dicembre e di giugno, che contengono i solstizi: la loro ampiezza è minima perché minima è la variazione in declinazione attorno ai solstizi; inoltre il loro settore si divide in una parte da rappresentare sul lato di declinazione ascendente e un’altra sul lato discendente.

