
L’apice dello stilo degli orologi solari è spesso dotato di uno schermo forato. Questo foro, che per tradizione è chiamato foro gnomonico, proietta sul quadro una macchiolina di luce rotondeggiante. Il foro gnomonico si utilizza ogniqualvolta la lunghezza dell’ombra dello gnomone sia, per qualche ragione, significativa.
Essendo il Sole una sorgente non puntiforme (il suo diametro apparente è di mezzo grado), le ombre proiettate dagli oggetti non hanno contorni nitidi e la larghezza della fascia di penombra che corre lungo il bordo di un’ombra è tanto maggiore quanto maggiore è la distanza dell’oggetto opaco dalla superficie su cui essa si proietta (vedi: effetti di ombra e penombra). In particolare se l’oggetto ha la forma di un bastoncino sottile non è agevole trovare il punto preciso dell’ombra corrispondente al suo apice.
Anche la macchiolina luminosa proiettata dal foro soffre della sfocatura dei bordi ma è comunque più facile individuare la posizione del centro di una macchiolina rotondeggiante piuttosto che dover individuare il punto in cui termina l’estremità dell’ombra di uno stilo.
L’aspetto più interessante del foro gnomonico è che ad una distanza limite (pari a $\text{114,6}$ volte il diametro del foro) la fascia di penombra “invade” completamente la macchiolina di luce. Se il foro è circolare, l’unico punto della superficie di proiezione in cui il disco solare è completamente visibile è il centro della macchiolina. Oltre questa distanza, compare quasi per magia l’immagine capovolta del Sole. E’ questo l’effetto che sta alla base delle camere oscure. Da quel punto in poi il problema della “sfocatura” dei bordi diminuisce gradualmente con la distanza: maggiore è la distanza, migliore è la qualità dell’immagine del Sole. A questo punto subentra però un problema di luminosità: l’immagine del Sole diminuisce esponenzialmente di luminosità e, se l’ambiente circostante non è abbastanza buio, scompare presto alla nostra vista.
Gli gnomonisti conoscevano bene questo problema quando pensarono di costruire le meridiane a foro gnomonico all’interno delle chiese: le dimensioni e l’ambiente buio, riparato dalla luminosità diffusa del giorno, erano condizioni eccellenti per misurare con grande precisione la direzione dei raggi del Sole avendo la possibilità di osservare un’immagine nitida dell’astro proiettata sul pavimento ad una distanza di parecchi metri.
Le dimensioni e la forma della macchia di luce variano ulteriormente per il fatto che il foro e lo schermo non sono paralleli tra loro (il foro è verticale e lo schermo è di solito un piano orizzontale) ed entrambi non sono di solito perpendicolari ai raggi del Sole. Le situazione ideali per ridurre al minimo l’imprecisione di misura, alle quali si dovrebbe tendere quando si progetta uno strumento solare sono:
1) grande distanza tra il foro e lo schermo di proiezione
2) ambiente circostante riparato dalla luce diffusa
3) parallelismo tra il pano del foro e il piano di proiezione
4) perpendicolarità tra questi due piani e la direzione dei raggi solari.
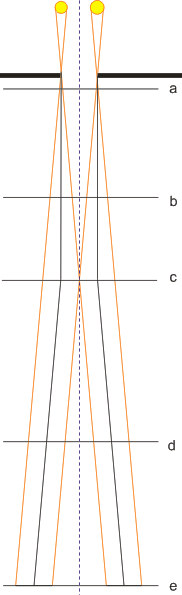
Il Sole non è una sorgente puntiforme, bensì è un disco che possiede un diametro angolare (apparente) di mezzo grado. Di conseguenza le ombre proiettate presentano aloni di penombra più o meno spessi a seconda della distanza tra l’oggetto opaco e lo schermo. In questo schema si rappresenta geometricamente il propagarsi dell’alone di penombra nel caso di un foro gnomonico. Le tracce da $a$ ad $e$ rappresentano degli schermi posti a varie distanze dal foro. Lo schermo $c$ si trova alla distanza limite di $\text{114,6}$ volte il diametro del foro (in questo disegno l’angolo di mezzo grado e le proporzioni non sono rispettate).
Il Sole non è una sorgente puntiforme ma possiede un diametro angolare (apparente) di mezzo grado. Di conseguenza le ombre proiettate presentano aloni di penombra più o meno spessi a seconda della distanza tra l’oggetto opaco e lo schermo. In questo schema si rappresenta geometricamente il propagarsi dell’alone di penombra nel caso di un foro gnomonico. Le tracce da $a$ ad $e$ rappresentano degli schermi posti a varie distanze dal foro. Lo schermo $c$ si trova alla distanza limite di $\text{114,6}$ volte il diametro del foro (in questo disegno l’angolo di mezzo grado e le proporzioni non sono rispettate).

Si rappresenta qui l’aspetto della macchia di luce in funzione della distanza tra un foro circolare di diametro $f$ e uno schermo parallelo ad esso.
Se il piano di proiezione si trova a distanze intermedie comprese tra le posizioni $a$ e $c$ la macchia di luce conserva la forma del foro ma lo spessore dell’alone di penombra lungo i suoi bordi aumenta con la distanza.
Alla distanza limite $c=\text{114,6}\cdot f$) la penombra “invade” interamente la macchia circolare ad esclusione del punto centrale.
A distanze maggiori della distanza limite (schermi $d$ ed $e$) compare l’ “effetto camera oscura“. L’alone mantiene uno spessore costante e uguale al diametro del foro. In questa zona la macchia di luce si trasforma nell’immagine capovolta del disco solare.
A conclusione, i risultati migliori si ottengono trovando empiricamente un buon compromesso tra l’altezza dello gnomone (tenendo in considerazione la distanza limite di $\text{114,6}f$), il diametro del foro e l’illuminazione dell’ambiente.
Vedi anche, Misurazione dell’ombra e problemi di penombra, Uso del foro gnomonico.
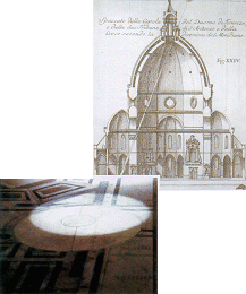
Esistono in Italia numerose chiese dotate di foro gnomonico che sfruttano l’effetto della camera oscura. La più famosa quella di Firenze in in Santa Maria del Fiore, alta 90 metri. L’ambiente semioscuro delle chiese ha permesso ai costruttori di ridurre al limite il diametro del foro gnomonico, aumentando di molto la precisione.
Vedi Uno studio sulla meridiana del Duomo di Milano (ITAS “Natta” MI)
Qui, trovate un elenco di 74 meridiane gnomoniche storiche italiane tratto da un documento di Giorgio Mesturini, per il XI Seminario Nazionale di Gnomonica.

