L’ombra della Terra proiettata sulla Luna durante un’eclisse lunare è di forma circolare e le sue dimensioni variano leggermente di eclisse in eclisse perché dipendono dalle distanze relative tra la Terra, la Luna e il Sole. In questa pagina si spiega come calcolare il raggio del cerchio d’ombra analizzando geometricamente la struttura del cono d’ombra: un cono circoscritto alla Terra e al Sole.
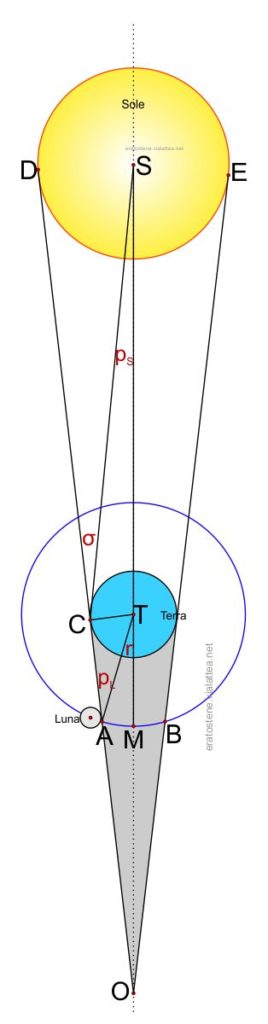
Nell’immagine, le cui proporzioni sono falsate per ragioni di chiarezza grafica, si rappresentano il Sole, la Terra al centro dell’orbita lunare, e la Luna nell’istante di inzio della sua immersione nel cono d’ombra. Quest’ultimo ha per vertice il punto “O”. Lo schema rappresenta quegli angoli che sono i parametri essenziali per il calcolo del raggio del cono d’ombra:
- $D\hat{C}S=\sigma$: il semidiametro apparente del Sole;
- $C\hat{A}T=P_L$: la parallasse della Luna;
- $C\hat{S}T=P_S$: la parallasse del Sole;
La sezione normale del cono d’ombra, in corrispondenza dell’arco di orbita lunare $AB$, è un cerchio il cui raggio apparente è l’angolo $M\hat{T}A=r$.
Innanzitutto possiamo notare che la semiapertura del cono d’ombra, cioè l’angolo $D\hat{O}S$, è facilmente calcolabile in base a $\sigma$ e $P_S$. Consideriamo infatti il triangolo $SCO$ e osserviamo che l’angolo $\sigma$ è uno degli angoli esterni di questo triangolo. Di conseguenza la sua misura è uguale alla somma dei due angoli non adiacenti ad esso; è possibile perciò calcolare l’ampiezza del cono d’ombra con una semplice sottrazione:
$D\hat{O}S=\sigma-P_S$
Con un’operazione simile, applicata al triangolo $TAO$ possiamo calcolare il raggio del cono d’ombra $r$. Infatti, l’angolo $P_L$ è esterno al triangolo $TAO$ e perciò:
$D\hat{O}S=P_L-r$
da cui:
$r=P_L-D\hat{O}S$
Ma sappiamo che $D\hat{O}S=\sigma-P_S$ e perciò possiamo scrivere infine:
$$\boxed{r=P_L+P_S-\sigma}$$
Le parallassi della Luna e del Sole e il semidiametro del Sole sono dati ricavabili dagli almanacchi e una semplice somma algebrica ci fornisce il raggio del cono d’ombra.

