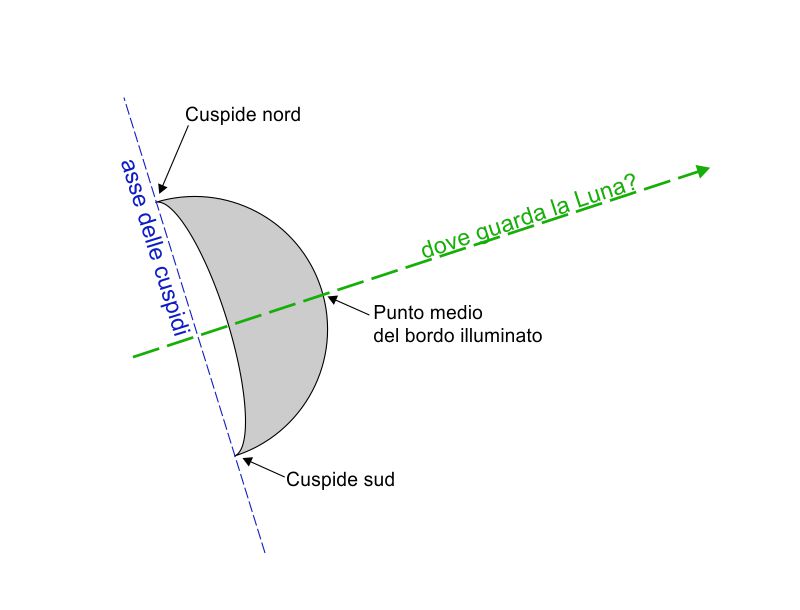
Se si osserva la Luna intorno al primo quarto o all’ultimo quarto si può assistere ad un fenomeno interessante. Il bordo illuminato dovrebbe essere rivolto verso il Sole. In termini più precisi, prolungando il segmento che congiunge il centro del disco lunare con il punto medio del bordo illuminato (o apice del bordo illuminato) si dovrebbe incontrare il Sole. L’asse delle cuspidi (chiamata anche linea dei corni) è perpendicolare al circolo massimo che passa per la Luna e il Sole.
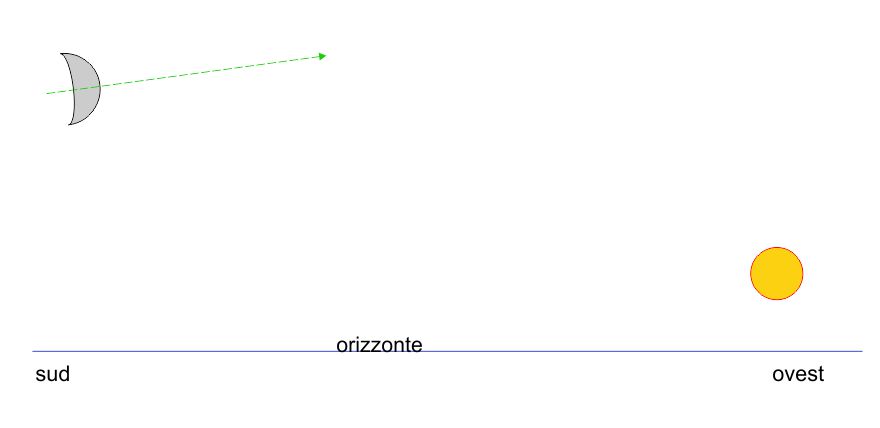
Eppure in alcune situazioni si può assistere ad una strana, apparente anomalia. Ad esempio, se la Luna è all’incirca al primo quarto e il Sole si avvicina al tramonto si può osservare che il punto medio del bordo illuminato è rivolto “verso l’alto” (*). La Luna, in questa situazione si trova certamente ad un’altezza maggiore del Sole e quindi, secondo logica, il bordo illuminato dovrebbe rivolgersi “verso il basso”, cioè verso l’orizzonte nel punto dove si trova il Sole. Sembra perciò che la Luna “non guardi” il Sole come dovrebbe.
Per verificare come stanno davvero le cose basta usare una corda. A braccia tese si tende la corda in modo che essa raggiunga sia il centro del disco lunare che il centro del disco solare. Si scoprirà che la corda è effettivamente allineata con la direzione dell’apice del bordo illuminato della Luna; ad occhio nudo è facile valutare anche la perpendicolarità della corda rispetto all’asse delle cuspidi lunari. Dobbiamo concludere che, nonostante le apparenze, la Luna sta effettivamente guardando il Sole!
Osservando senza l’uso di una corda, il nostro atteggiamento istintivo è quello di confrontare tra loro le altezze dei due astri e decidere quale dovrebbe essere la direzione dell’apice illuminato della Luna rispetto al Sole. In realtà, il confronto tra le altezze degli astri, in questo caso, non ci porta da nessuna parte.
La spiegazione del fenomeno ha a che fare con una questione squisitamente geometrica che riguarda la sfera celeste. La distanza angolare tra due corpi celesti corrisponde necessariamente ad un arco di cerchio massimo sulla sfera. Se si vuole tracciare il percorso più breve tra due punti sulla superficie di una sfera è necessario far passare per i due punti un cerchio massimo. Qualunque altro arco, tracciato lungo cerchi minori, sarà più lungo dell’arco di cerchio massimo. Il percorso della luce solare che illumina la Luna è il percorso più breve tra i due astri e perciò la direzione da cercare in cielo è quella dell’arco di cerchio massimo.

La distanza angolare tra due astri è concettualmente facile da misurare: l’occhio ($O$) rappresenta il centro della sfera celeste e l’angolo compreso tra le direzioni dei due astri $\widehat{LOS}$ corrisponde anche all’arco di cerchio massimo $a$ che passa per essi. Tale arco è la proiezione sulla sfera celeste della linea retta che li congiunge effettivamente ($LS$), ed è anche la proiezione sulla sfera celeste della corda $c$ tesa tra le nostre mani mentre si esegue l’osservazione descritta precedentemente.

Per capire meglio l’apparente anomalia osservata si pensi ad una situazione semplificata in cui la Luna, vicina al primo quarto, e il Sole, si trovino alla stessa altezza. E’ una situazione che si verifica effettivamente ad una certa ora pomeridiana quando il Sole si trova nell’emisfero occidentale e la Luna nell’emisfero orientale a circa $90^\circ$ di distanza angolare. In questo istante c’è un unico almucantarat che passa per entrambi gli astri. L’almucantarat, o parallelo di altezza è un cerchio minore, parallelo all’orizzonte, i cui punti hanno la stessa altezza. Di conseguenza l’arco di almucantarat che congiunge i due astri non è la loro distanza angolare. L’immagine qui a fianco rappresenta l’idea erronea che abbiamo di uno sfondo piatto del cielo in cui l’almucantarat e l’orizzonte sembrano due rette parallele. Così si immagina che la distanza tra i due astri sia un arco di almucantarat.
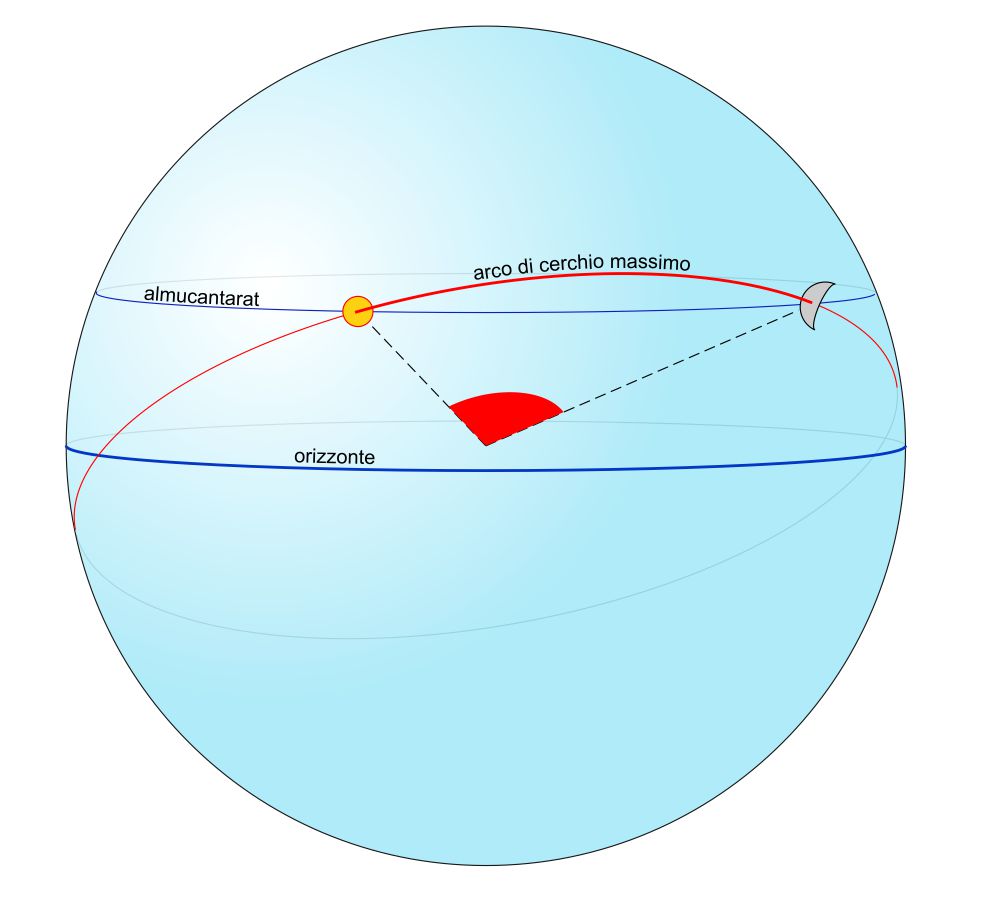
L’arco di cerchio massimo che congiunge i due astri passa al di sopra dell’almucantarat. Ciò spiega la strana inclinazione “verso l’alto” della gobba lunare che ci fa credere che la Luna non stia “guardando” il Sole.
Ringrazio Valerio Versari per il suo utile contributo a questa pagina.
L’assetto del bordo illuminato e quindi dell’asse delle cuspidi lunari si può calcolare in base alle coordinate equatoriali del Sole e della Luna e alla latitudine dell’osservatore. Descrivo qui l’algoritmo (da Meeus, Astronomical Algorithms, 2009).
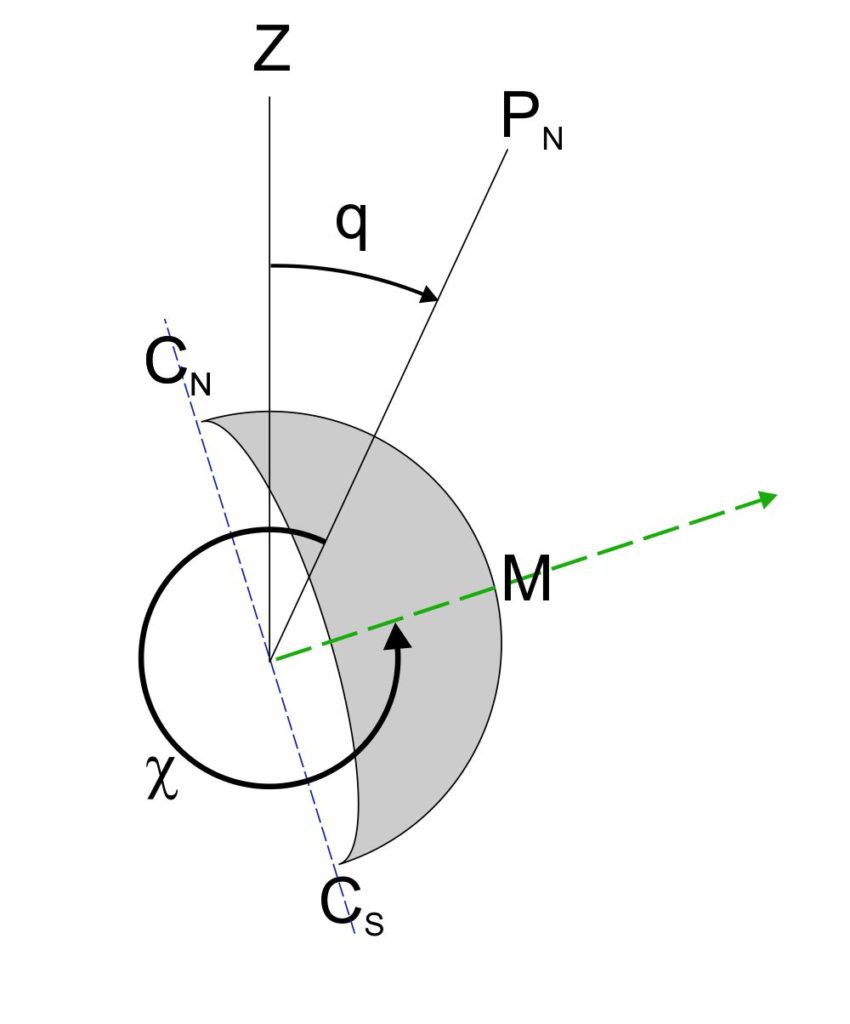
$C_N$ e $C_S$: cuspidi nord e sud
$M$: punto medio del bordo illuminato
$Z$: direzione dello zenit
$P_N$: direzione del polo nord celeste
$\chi$: posizione angolare del punto medio rispetto al punto nord del disco lunare
$q$: angolo parallattico
L’angolo $\chi$ si calcola:
$$\tan\chi=\frac{\cos\delta_S\sin(\alpha_S-\alpha_L)}{\sin\delta_S\cos\delta_L-\cos\delta_S\sin\delta_L\cos(\alpha_S-\alpha_L)}$$Dove $\alpha_S$, $\delta_S$ e $\alpha_L$, $\delta_L$ sono l’ascensione retta e la declinazione rispettivamente del Sole e della Luna.
L’angolo di posizione $\chi$ fornisce l’inclinazione dell’apice del bordo illuminato rispetto alla direzione del polo nord celeste. Per trovare l’angolo di posizione rispetto allo zenit $\chi_z$:
$$\chi_z = \chi-q$$dove $q$ è l’angolo parallattico.
L’angolo di posizione delle cuspidi si ottiene sommando o sottraendo $90^\circ$ a $\chi$ o a $\chi_z$ rispettivamente per la cuspide nord e la cuspide sud.

