Un esempio di calcolo della longitudine solare
In questo esempio, basato su dati attuali, immaginiamo di voler calcolare la longitudine eclittica vera del Sole per una certa data come il 24 agosto del 2022 alle ore 12.
Abbiamo a disposizione i seguenti dati:
– la lunghezza dell’anno tropico ($\text{365,2422}$ giorni)
– l’eccentricità $\epsilon=\text{0,0334}$
– la longitudine dell’apogeo $L_a=\text{103,74}^\circ$)
Abbiamo a disposizione anche una formula per calcolare l’equazione del centro $E_c$ in base all’anomalia media $\alpha_m$ e all’eccentricità e sappiamo che l’anomalia media si ottiene dalla longitudine media $\lambda_m$ e dalla longitudine dell’apogeo $L_a$ con una semplice operazione:
$$\alpha_m = \lambda_m – L_a$$
e, dato che $E_c=\alpha_v-\alpha_m$ si può calcolare $\alpha_v$ ed infine la longitudine vera $\lambda_v$:
$$\lambda_v=\alpha_v+L_a$$
Perciò il vero dato mancante è la longitudine media $\lambda_m$ del Sole il 24 agosto del 2022. Come fare?
La longitudine media del Sole aumenta ogni giorno di un valore costante pari a $\frac{360^\circ}{\text{365,2422}}=\text{0,9856}^\circ$. Perciò, se conoscessimo la longitudine media di una certa data si potrebbe facilmente calcolare la longitudine media di qualsiasi altra data successiva o precedente, aggiungendo o togliendo $\text{0,9856}^\circ$ al giorno. Ebbene, se si misura con precisione l’istante di un solstizio o di un equinozio, conosciamo anche la longitudine vera di quell’istante ($\lambda_v$ è $0^\circ$, $90^\circ$, $180^\circ$ e $270^\circ$ rispettivamente all’equinozio di marzo, al solstizio di giugno, all’equinozio di settembre e al solstizio di dicembre). Con il procedimento matematico che segue, si può calcolare la longitudine media $\lambda_m$ di uno di questi istanti, e da questa, la longitudine media della data che ci interessa.
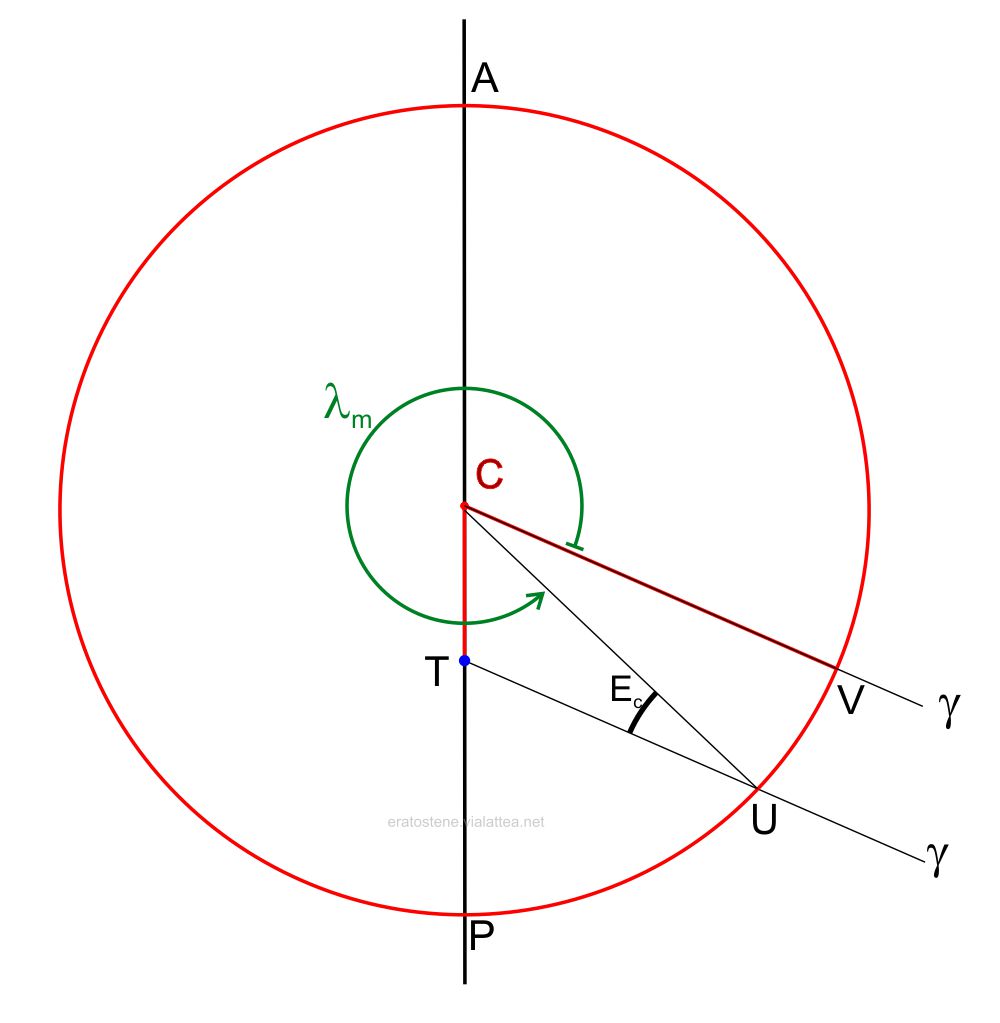
Qui è rappresentata la situazione all’equinozio di marzo. Il punto vernale $\gamma$ si trova a distanza praticamente infinita rispetto alla Terra $T$ e al centro del cerchio del Sole $C$. Perciò le due semirette $CV$ e $TU$ rappresentano la direzione del punto vernale visto rispettivamente dal Sole e dalla Terra. All’equinozio di marzo il Sole vero, visto da $C$ è in $V$, la sua longitudine è $0^\circ$. Il Sole medio, invece, è rimasto un po’ indietro, non ha ancora completato i $360^\circ$. Gli manca l’angolo $U\hat{C}V$ che è uguale al valore dell’equazione del centro $E_c$ per quella data.
Conosciamo la longitudine vera del Sole all’equinozio di marzo ($\lambda_v=0^\circ$), conosciamo perciò l’anomalia vera $\alpha_v$ alla stessa data, perché la longitudine dell’apogeo ci è nota ($L_a=\text{103,74}^\circ$):
$$\alpha_v = \lambda_v – L_a=360^\circ-\text{103,74}^\circ=\text{256,26}^\circ$$
A questo punto, si tratta di trovare un modo per calcolare l’equazione del centro $E_c$ in funzione dell’anomalia vera $\alpha_v$ ed il problema è risolto.
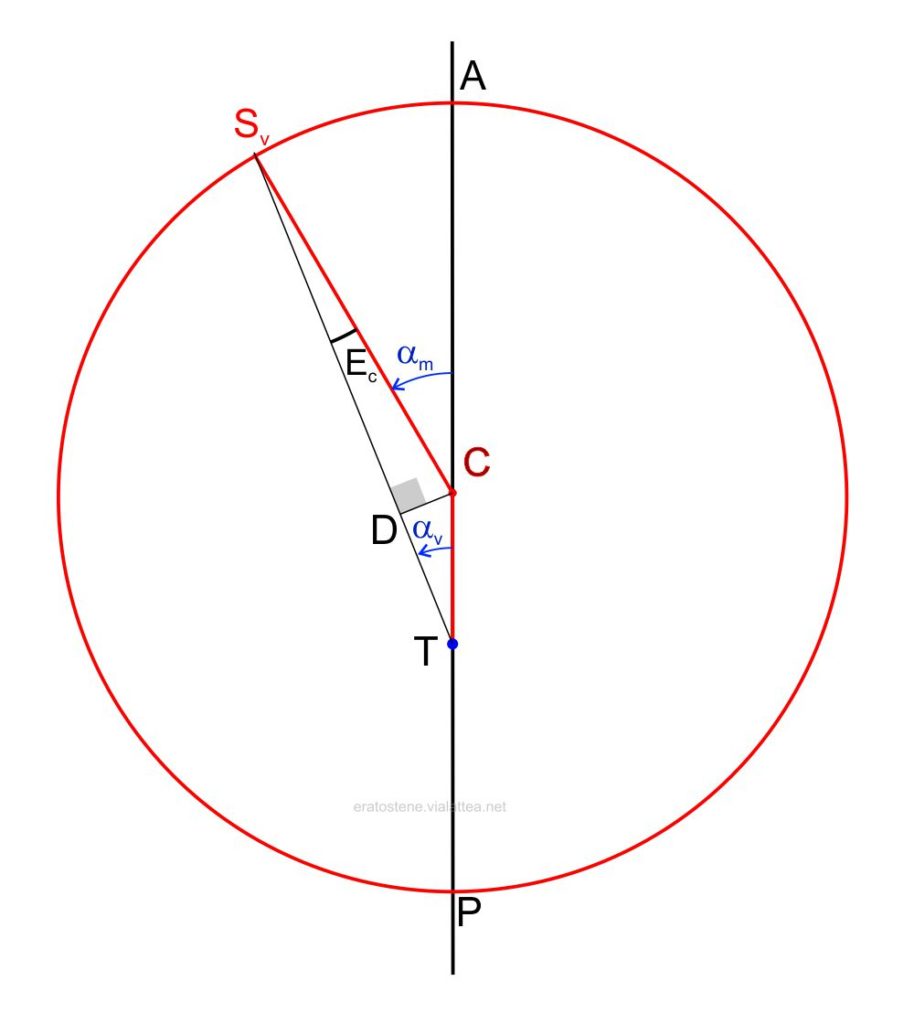
Qui riproduciamo una situazione qualsiasi: il Sole vero in $S_v$, la sua anomalia media $\alpha_v$, e l’equazione del centro $E_c$. Tracciamo il segmento $CD$ perpendicolare a $S_vT$ e otteniamo due triangoli rettangoli retti in $D$: il triangolo $CDT$ e il triangolo $S_vDC$. Dal primo triangolo otteniamo la misura di $CD$:
$$CD = CT\cdot\sin{\alpha_v}$$
Operando sul secondo triangolo, la cui ipotenusa $S_v$ è unitaria, otteniamo $E_c$:
$$\sin{E_c}=CD = CT\cdot\sin{\alpha_v}$$
Considerando che $E_c$ in questo settore di anomalia è negativo, e che $CT$ è l’eccentricità $\epsilon$ ecco la formula definitiva che ci permette il calcolo dell’equazione del centro $E_c$ in funzione dell’anomalia vera $\alpha_v$:
$$\boxed{\sin{E_c}= – \epsilon\cdot\sin{\alpha_v}}$$
Procediamo ora con i nostri calcoli. Immaginiamo innanzitutto di aver misurato con buona precisione l’istante dell’equinozio di marzo 2022:
20 marzo 2022, ore 15:33
Calcoliamo l’anomalia vera, l’equazione del centro dell’istante dell’equinozio e la longitudine media:
$$\alpha_v = \lambda_v – L_a=360^\circ-\text{103,74}^\circ=\text{256,26}^\circ$$
$$E_c=-\epsilon\cdot\sin{\alpha_v}=-\text{0,0334}\cdot\sin{\text{256,26}^\circ}=\text{1,8589}^\circ$$
$$\lambda_m=\lambda_v-E_q=360^\circ-\text{1,8589}^\circ=\text{358,14}^\circ$$
Dall’equinozio di marzo 2022 al 24 agosto 2022 ore 12 sono trascorsi 156 giorni e 20 ore e mezzo, cioè $\text{156,85}$ giorni.
La longitudine media, in questo periodo, è aumentata di:
$\text{156,85}\cdot\frac{360^\circ}{\text{365,2422}}=\text{154,60}^\circ$
Perciò la longitudine media del 24 agosto 2022 alle ore 12 è:
$$\text{358,14}^\circ+\text{154,60}^\circ=\text{152,74}^\circ$$
L’anomalia media al 24 agosto alle ore 12 è:
$$\alpha_m=\lambda_m-L_a=\text{152,74}^\circ-\text{103,74}^\circ=\text{49,00}^\circ$$
L’equazione del centro al 24 agosto ore 12 è:
$$\sin{E_c}=-\frac{\epsilon\cdot\sin{\alpha_m}}{\sqrt{1+2\epsilon\cdot\cos{\alpha_m}+\epsilon^2}}$$
$$\sin{E_c}=-\frac{\text{0,0334}\cdot\sin{49^\circ}}{\sqrt{1+2\cdot\text{0,0334}\cdot\cos{49^\circ}+\text{0,0334}^2}}=-\text{0,02466}$$
da cui $E_c=\text{-1,4129}^\circ$.
Con quest’ultimo valore possiamo finalmente calcolare la longitudine vera del Sole il 24 agosto 2022 alle ore 12:
$\lambda_v=\lambda_m+E_c=\text{152,74}^\circ+(\text{-1,4129}^\circ)=\text{151,3271}^\circ=151^\circ19’38^{”}$
Il valore ottenuto con pyephem è $151^\circ19’25^{”}$. Tolomeo avrebbe ottenuto un risutato soddisfacente!