Il modello del cerchio eccentrico
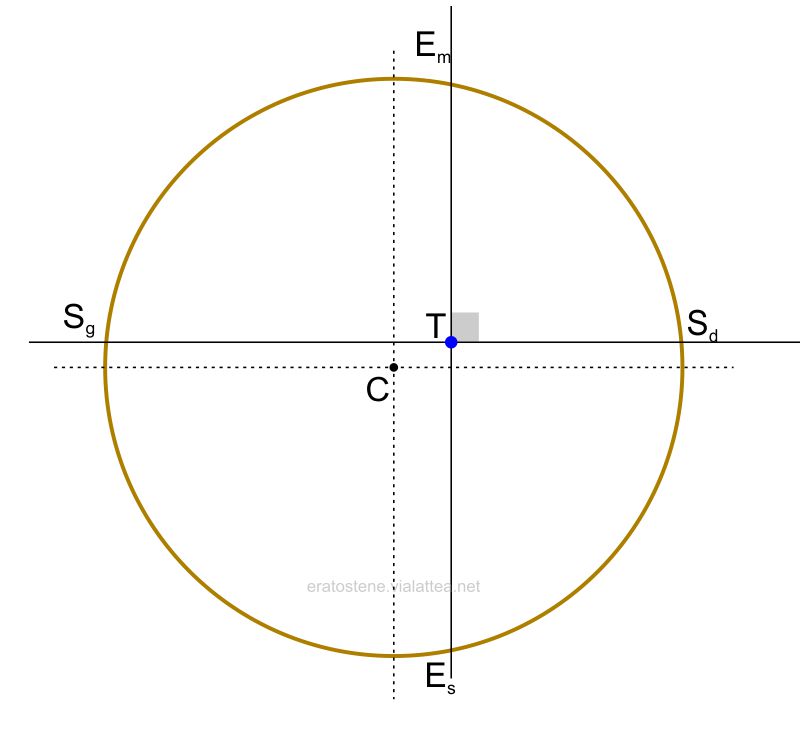
Se dovessimo spiegare l’anomalia solare attuale con il modello del cerchio eccentrico, si dovrebbe posizionare la Terra $T$ in un punto nel settore dell’inverno boreale (tra $S_d$ e $E_m$) ad una certa distanza $CT$ dal centro dell’orbita Solare. In questo modo possiamo supporre che il Sole si muova lungo l’eclittica con moto costante ma il suo moto apparente, cioè visto dalla Terra, varierebbe nel corso dell’anno essendo più lontano da noi durante l’estate boreale, nell’arco da $S_g$ a $E_s$, e più vicino durante l’inverno nel suo percorso da $S_d$ a $E_m$.

Tracciando una retta che passa per il centro $C$ dell’orbita solare e per la Terra $T$, si ottiene la linea degli apsidi, che interseca l’eclittica nei due nodi chiamati perigeo $(P)$ e apogeo $(A)$ nel modello geocentrico. Essi sono i due punti dell’eclittica in cui il Sole raggiunge rispettivamente la minima e la massima distanza dalla Terra. Il perigeo dovrebbe essere attraversato dal Sole alcuni giorni dopo il solstizio di dicembre mentre l’apogeo alcuni giorni dopo il solstizio di giugno (nel modello eliocentrico attuale, quesi due punti sono chiamati afelio e perielio).
Tale posizione eccentrica dell’orbita solare rispetto al centro dell’universo che è la Terra, riesce a spiegare la diversità delle stagioni che in ordine di durata sono l’estate, la primavera, l’autunno e l’inverno boreali.
L’angolo $E_m \hat{T}A$ è chiamato longitudine dell’apogeo e il rapporto $\frac{CT}{CA}$ è chiamato eccentricità. La logitudine dell’apogeo decide quale stagione è la più lunga e quale è la più corta, l’eccentricità determina il grado di diversità tra le durate delle stagioni.
Misurando quattro parametri: la lunghezza dell’anno tropico, l’eccentricità, la longitudine dell’apogeo e la longitudine del Sole, si possono prevedere le posizioni future del Sole.

