Il punto del sorgere e il punto del tramonto del Sole sono legati alla sua declinazione e alla latitudine del luogo. Da questi due importanti parametri dipendono anche la lunghezza dell’arco diurno del Sole. Se la lunghezza dell’arco diurno varia, variano anche le ore di illuminazione perché la velocità del moto diurno apparente del Sole, cioè la sua variazione di angolo orario è praticamente costante.
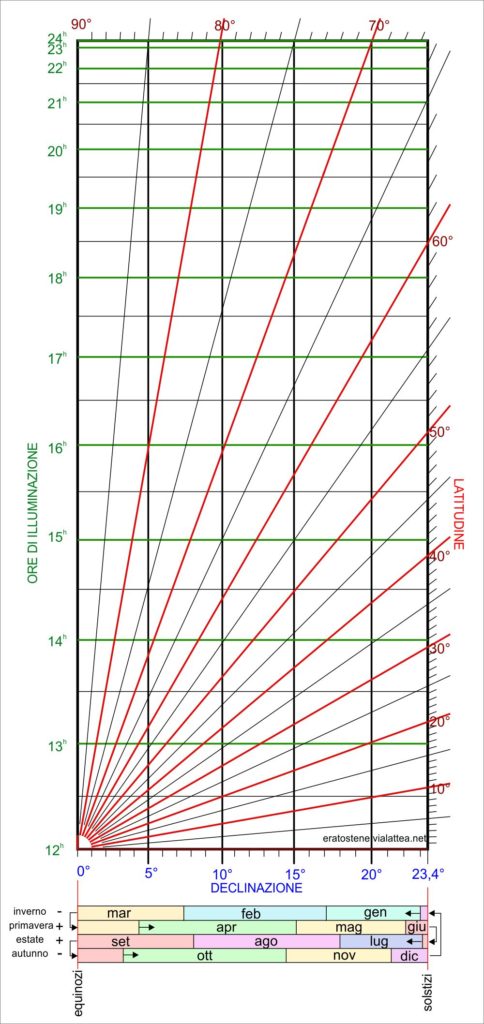
Questo grafico permette una rapida valutazione, anche se approssimata, delle ore di luce in base alla declinazione del Sole (e perciò al periodo dell’anno) e alla latitudine.
Per conoscere la declinazione in base alla data si può usare il grafico dei mesi sottostante suddiviso in quattro segmenti stagionali. I segni $+$ e $-$ a fianco indicano se la declinazione è da considerarsi positiva o negativa per le corrispondenti stagioni boreali. Un’alternativa più precisa consiste nel consultare queste tavole di declinazione.
Per determinare il numero di ore di illuminazione si cerca l’intersezione tra la retta verticale corrispondente al valore della declinazione scelta in ascissa e la retta inclinata corrispondente alla latitudine del luogo. Questo punto di intersezione fornisce, sull’asse delle ordinate il numero di ore di luce. Ciò vale per le latitudini nord e per le declinazioni positive.
Se la declinazione è negativa si esegue lo stesso procedimento ma il valore trovato in ordinata non indica le ore di luce, bensì quelle di buio, cioè la durata della notte.
Se la latitudine è di specie sud la lettura è nuovamente rovesciata (le declinazioni negative indicano le ore di luce e quelle positive le ore di buio).
La tavola può essere scaricata in formato pdf e stampata:
Esempio 1: per una località a $62^\circ$ di latitudine boreale, quante ore di luce ci sono il 20 novembre?
Osservando diagramma dei mesi, il 20 novembre corrisponde ad una declinazione di circa $-20^\circ$ (l’autunno boreale ha decliazione negativa). La retta verticale che si trova sui $20^\circ$ interseca la retta inclinata di latitudine $62^\circ$ ad un’altezza che corrisponde a circa $17^h30^m$. Essendo la declinazione negativa, questa lettura corrisponde al numero di ore di buio. Perciò le ore di illuminazione sono:
$$24^h-17^h30^m=6^h30^m$$
Con questo dato possiamo anche calcolare l’ora solare vera del sorgere e del tramonto del Sole, dato che le ore di illuminazione si dispongono equamente a cavallo del mezzogiorno:
$$12^h-\frac{6^h30^m}{2}=8^h45^m$$
$$12^h+\frac{6^h30^m}{2}\simeq15^h15^m$$
Perciò il Sole sorge alle ore $8:45$ e tramonta alle ore $15:15$ (ora solare vera).
Esempio 2: il giorno del solstizio dell’estate australe (solstizio di dicembre) quante ore di luce ci sono a Cape Town (Sudafrica)?
Cape Town si trova alla latitudine australe di $34^\circ$. Il giorno del solstizio di dicembre corrisponde ad una declinazione di $-\text{23,4}^\circ$ perciò la lettura del punto di intersezione della verticale destra con la retta di latitudine $34^\circ$ ci fa leggere all’incirca $14^h20^m$, un valore che, in questo caso, indica le ore di luce.
Calcoliamo l’alba e il tramonto allo stesso modo:
$$12^h-\frac{14^h20^m}{2}\simeq4^h50^m$$
$$12^h+\frac{14^h20^m}{2}\simeq19^h10^m$$
La formula che permette di calcolare con precisione le ore di luce e sulla quale è basata la costruzione del nostro grafico (1) è la seguente:
$$\boxed{\cos \widehat{P}=-\tan\varphi\cdot\tan\delta}$$
dove $\widehat{P}$ è l’angolo al polo del Sole all’orizzonte nell’istante del suo sorgere o del suo tramontare, $\varphi$ è la latitudine e $\delta$ la declinazione.
L’angolo al polo di un astro all’orizzonte è in pratica il suo semiarco diurno e quindi, nel caso del Sole, esso rappresenta la metà delle ore di luce.
La formula non fornisce sempre un valore di coseno calcolabile: infatti, se $-\tan\varphi\cdot\tan\delta$ è minore di $-1$, significa che il Sole appartiene alla calotta di perenne visibilità, viceversa, se è maggiore di $+1$ il Sole non sorge mai (vedi astri circumpolari e astri anticircumpolari). Un limite analogo lo si incontra utilizzando la tabella per la quale, oltre i $\text{66,6}^\circ$ di latitudini nord o sud, che sono i limiti dei circoli polari, le declinazioni vicine al bordo destro dei solstizi (dove $\delta=\text{23,4}^\circ)$ non forniscono un’intersezione utile per la determinazione delle ore di luce: il limite è il bordo superiore del rettangolo che indica $24$ ore di luce o di buio.
Suggerisco la pagina Motions of the Sun, un’ottima simulazione che, più di tante parole, ci fa capire la relazione tra declinazione del Sole, latitudine durata del dì e della notte.
La prossima pagina è dedicata a chi apprezza le spiegazioni complete, e contiene la dimostrazione della formula.
(1)
Indicazioni per costruire la tavola delle ore di luce.
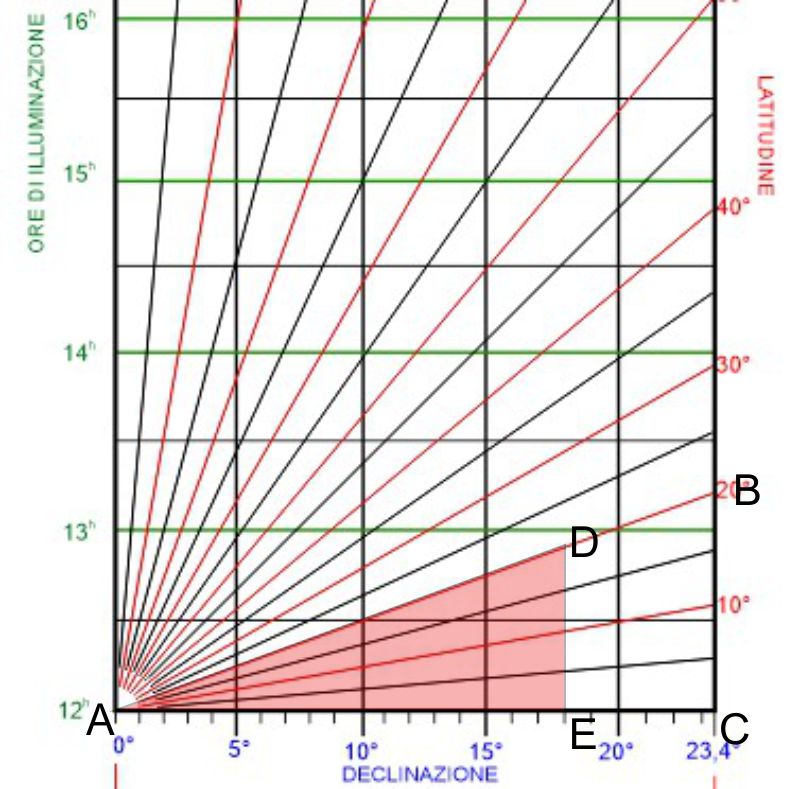
Le declinazioni segnate in ascissa sono disposte su una scala delle loro tangenti, adeguatamente proporzionata in base al foglio che si utilizza per disegnare (l’altezza della tavola finale risulterà all’incirca $\text{2,5}$ volte la larghezza). Ugualmente, la scala della latitudine, costruita con un goniometro centrato nell’angolo in basso a sinistra da dove si dipartono le rette inclinate, è una scala di tangenti delle latitudini basata sulla distanza $AC$ come raggio unitario.
In questo modo, qualsiasi retta verticale, corrispondente ad una certa declinazione, incontra la retta obliqua della latitudine in un punto $D$ la cui ordinata $DE$ si proporziona automaticamente in base al rapporto $AE/AC$. Essendo $AC=1$:
\begin{split}
DE&=BC\cdot AE\\
&=\tan\varphi\cdot\tan\delta\\
&=-\cos \widehat P
\end{split}
La scala delle ore di luce è perciò una scala di coseni. Le tacche da $12^h$ a $24^h$ sono state individuate calcolando le latitudini $\varphi$ per i valori di ore di illuminazione $i$ scelti, con la formula inversa:
$$\tan\varphi=-\frac{\cos \left(\frac{i}{2}\right)}{\tan\text{23,4}^\circ}$$
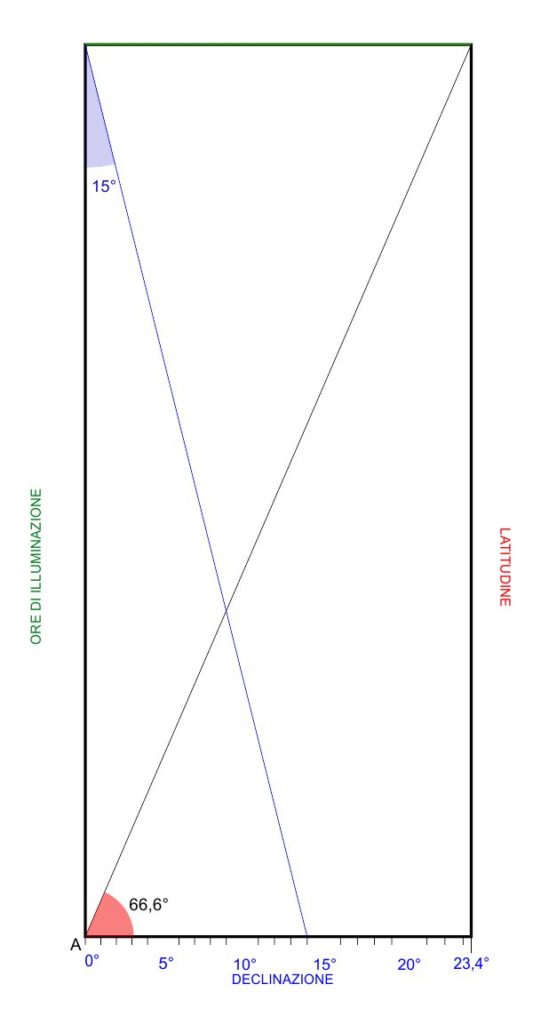
La scala della declinazione può essere costruita come prima operazione quando si imposta il grafico, in questo modo:
1) Si traccia la retta di latitudine $\text{66,6}^\circ$ che parte dal vertice $A$, allo scopo di individuare il vertice in alto a destra della tabella e si costruisce così il rettangolo di cornice del grafico;
2) Partendo dal vertice in alto a sinistra della cornice si tracciano le semirette delle declinazioni la cui ampiezza va misurata rispetto alla verticale: le loro intersezioni con la base della cornice individuano i punti di declinazione della scala. Nell’immagine è disegnata come esempio la semiretta della declinazione $15^\circ$.
- Orbita, eclittica, equatore
- Lo zodiaco: segni e costellazioni
- Stagioni
- Punto del sorgere e punto del tramonto del Sole
- Fotografare le variazioni di amplitudine
- Le ore di illuminazione
- Linea diurna e sezione conica
- Levata eliaca e tramonto eliaco
- Passaggi al meridiano e culminazioni
- Movimento apparente delle stelle circumpolari
- Moto diretto e retrogrado
- Oscillazioni dell’asse terrestre
- Aberrazione della luce
- La teoria solare tolemaica

