Nel II secolo a.C. Ipparco scoprì la precessione degli equinozi confrontando una misura della longitudine di Spica, da lui effettuata, con quella registrata da Timocaride di Alessandria e Aristillo centocinquant’anni prima; entrambe le misurazioni furono eseguite in occasione di eclissi lunari(1). Egli valutò un moto di precessione di almeno $1/100^\circ$ all’anno. Proviamo anche noi a confrontare una mappa storica con una mappa attuale. Effettueremo il confronto per mezzo di un espediente esclusivamente grafico che, pur approssimato, ci fornirà un esempio di stima della precessione. Una stima certamente grossolana ma che in compenso non fa uso di formule.
Utilizziamo le mappe di Uranografia, la famosa opera di Johann Bayer pubblicata per la prima volta nel 1603. Scegliamo anche noi, come fece Ipparco, la stella Spica. Questo astro ha il vantaggio di trovarsi nei pressi del punto omega e di essere anche vicina all’eclittica. Perciò andiamo ad esaminare in dettaglio la bellissima tavola che rappresenta la costellazione della Vergine. (Immagine da skytonight.org)
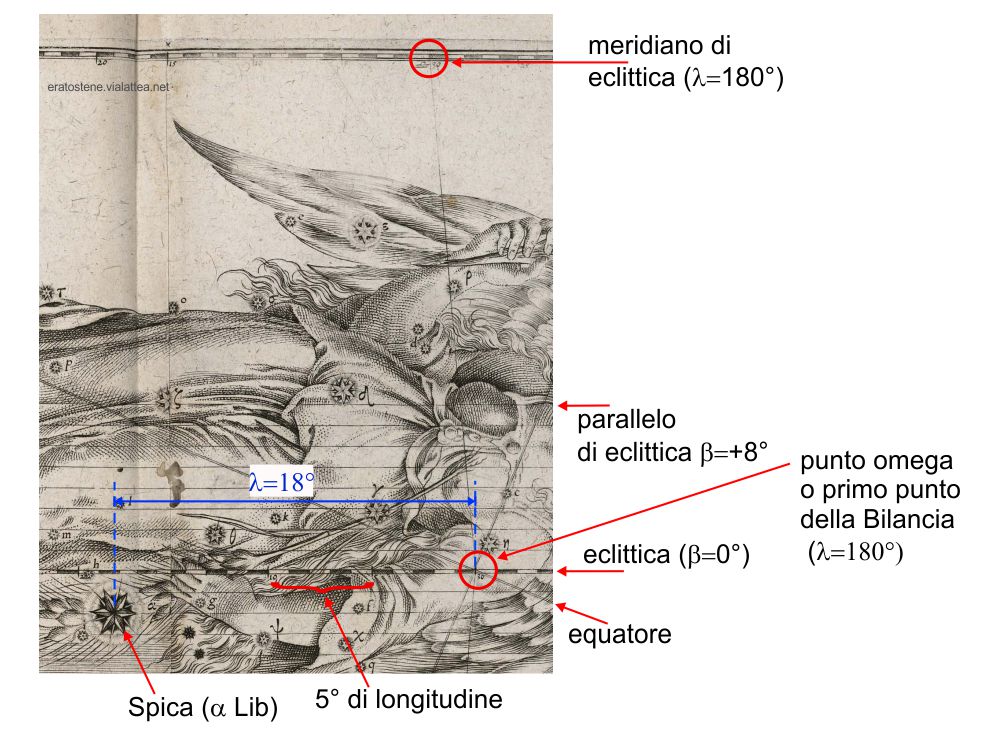
La rete disegnata da Bayer è quella dei meridiani e dei paralleli di eclittica. Si individua facilmente il punto omega, incrocio tra l’eclittica e l’equatore, e altrettanto facilmente si può capire la scala di longitudine utilizzata: si tratta della tipica scala zodiacale basata sulla suddivisione dell’eclittica in settori di $30^\circ$, usata fino al diciottesimo secolo. Quello che stiamo osservando nel dettaglio è la parte iniziale della casa della Bilancia, una fascia “rettangolare” compresa tra i meridiani celesti di longitudini $\lambda=180^\circ$ e $\lambda=210^\circ$ e tra i paralleli $\beta=-8^\circ$ e $\beta=+8^\circ$. La fascia dello Zodiaco è riconoscibile nelle mappe di Bayer per il colore più scuro.
La longitudine di Spica, secondo le mappe di Bayer, è all’incirca $18^\circ$ della Bilancia, cioè $\lambda=180^\circ + 18^\circ=198°$.

Le moderne mappe stellari sono disegnate sulla rete del sistema equatoriale e quindi il confronto non è immediato (qui, le linee verticali sono circoli orari e quelle orizzontali sono paralleli di declinazione). Ma un piccolo stratagemma grafico ci permette di ricavare la longitudine eclittica della posizione attuale di Spica. Puntando il compasso sul punto omega tracciamo un arco dalla posizione di Spica fino ad incontrare l’equatore e misuriamo così la distanza angolare di questo punto dal punto omega. In pratica, utilizziamo la scala di ascensione retta per misurare un arco di eclittica. Il trucco ha senso perché le due scale sono identiche essendo entrambe basate sulla suddivisione di circoli massimi. Troviamo che tale distanza è di circa $1^h35^m$ pari a $23.7^\circ$. Di conseguenza la longitudine è di circa $\lambda=180^\circ+23.7^\circ=203.7^\circ\simeq204^\circ$. (2)
Esaminiamo questa differenza di longitudine di $204^\circ-198^\circ=6^\circ$ . La mappa recente è datata 2011 mentre la data della mappa di Bayer è stata compilata partendo da un catalogo stellare di Tycho Brahe del 1598 anche se l’immagine che abbiamo esaminato si riferisce ad una stampa del 1661. Per i nostri scopi dimostrativi, le due incertezze non ci preoccupano molto e prendiamo per buono un intervallo di circa 400 anni. In questi quattro secoli la longitudine di Spica è aumentata di circa $6^\circ/400\simeq54^{”}$ all’anno equivalenti a $1.5^\circ$ al secolo $(1^\circ$ ogni 67 anni). La misura attuale di precessione è di $50.26^{”}$ all’anno che corrispondono a $1^\circ$ ogni $72$ anni. Il nostro semplice confronto grafico non tradisce. Con metodi analoghi a quello che abbiamo usato qui, è possibile datare approssimativamente una mappa o uno strumento antico di cui non si conosce l’autore.
- Precessione degli equinozi
- Precessione dell’equatore
- Nutazione
- Trovare la precessione nelle mappe storiche
La longitudine del Sole, cioè la sua distanza angolare dal punto gamma, si calcolava indipendentemente dalla posizione su posizione rispetto alle “stelle fisse“. La teoria solare di Ipparco e Tolomeo permetteva di prevedere con buona approssimazione la posizione del Sole sull’eclittica partendo da poche informazioni: i parametri necessari erano le date degli equinozi e dei solstizi e quindi la durata delle stagioni. Non potendo osservare contemporaneamente le stelle e il Sole, l’unico modo possibile per misurare la posizione delle stelle rispetto al Sole era quello di utilizzare le eclissi di Luna. Infatti in queste particolari occasioni il centro dell’ombra terrestre proiettata sulla Luna ha una longitudine che differisce da quella del Sole di $180^\circ$ esatti ed è rispetto a questo punto che si possono misurare agevolmente le posizioni delle stelle che si trovano nei dintorni della Luna e quindi determinare le loro coordinate eclittiche.
(2)Questo metodo presuppone numerose approssimazioni. In particolare, i tratti di meridiani e paralleli disegnato sulle mappe non sono rettilinei ma generalmente sono archi di cerchio o di ellissi (a seconda della proiezione). In ogni caso, nell’ambito di piccole regioni stellari nei pressi dell’equatore e dell’eclittica, questi archi si possono approssimare a tratti rettilinei misurabili con un semplice righello. E’ ciò che abbiamo fatto noi in questo “giochino” grafico.

