- Precessione degli equinozi
- Precessione dell’equatore
- Nutazione
- Trovare la precessione nelle mappe storiche
La precessione dell’equatore è la componente principale della precessione degli equinozi. E’ chiamata anche precessione luni-solare perché è dovuta all’azione gravitazionale della Luna e del Sole sul rigonfiamento equatoriale della Terra.
La scoperta del fenomeno è attribuita a Ipparco, intorno al $130$ a.C., confrontando le posizioni delle stelle principali osservate da lui, con quelle di cataloghi di un secolo e mezzo più vecchi. Egli si accorse che la longitudine eclittica di tutte le stelle era aumentata, progredendo di $\text{36”}$ all’anno (la stima attuale è $\text{50”}$ circa), mentre la loro latitudine eclittica era rimasta uguale.
L’interpretazione di Ipparco è stata che l’equatore celeste, e di conseguenza il punto vernale ($\gamma$), si muovono rispetto all’eclittica. Dato che la latitudine eclittica non varia, è da ritenere che l’eclittica, e quindi il suo polo ($\pi$) siano riferimenti stabili rispetto alle stelle, mentre l’equatore e il suo polo ($P$) non lo siano.
Ipparco non aveva evidenziato una variazione dell’obliquità dell’eclittica; se il punto vernale si muove, anche il polo celeste si muove conformemente, mantenendo la stessa distanza sferica (attualmente di circa $\text{23,4}^\circ$) dal polo dell’eclittica e descrivendo attorno ad esso un cerchio minore.
Se il punto vernale retrocede di circa $\text{50”}$ all’anno, una rotazione completa del polo celeste attorno al polo dell’eclittica impiega circa $26\,000$ anni.
$$(360\cdot 60\cdot 60)\text{”} : \text{50”} = 25\,920 anni$$
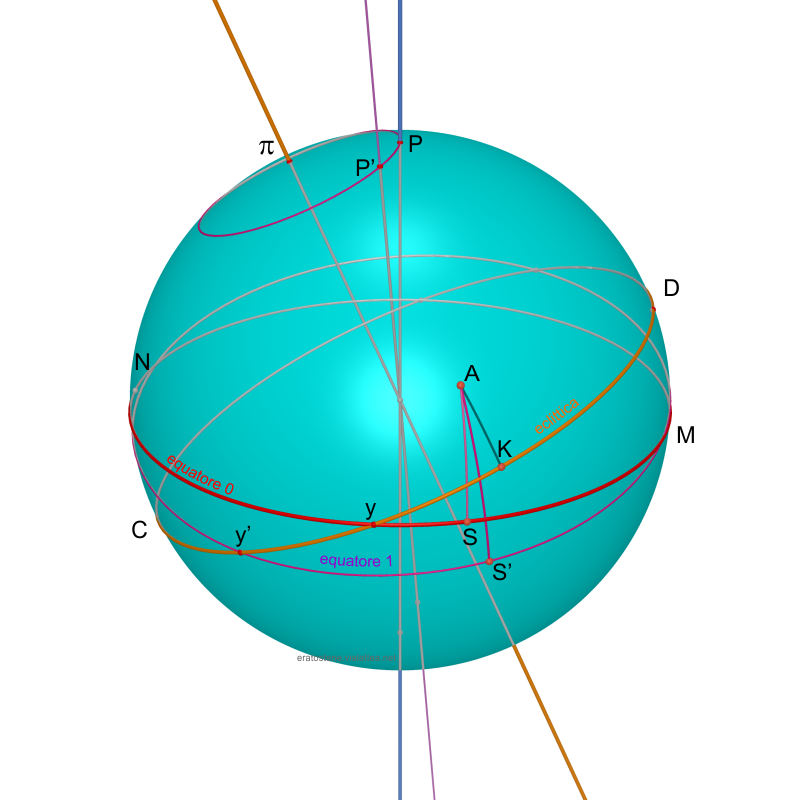
La figura rappresenta la variazione della posizione dell’equatore nel corso di un certo periodo.
$P$ è il polo nord celeste e $N\gamma M$ è il relativo equatore (equatore 0) ad una data iniziale. $P’$ è la nuova posizione del polo nord celeste dopo un certo tempo $t$, e $N\gamma’M$ è il nuovo equatore corrispondente (equatore 1). Il punto $\pi$ è il polo boreale dell’eclittica che rimane nella stessa posizione.
Osserviamo che il punto vernale, originariamente alla posizione $\gamma$ si è spostato lungo l’eclittica assumendo la nuova posizione $\gamma’$. Di conseguenza la longitudine eclittica di una stella $A$ è aumentata da $\gamma K$ a $\gamma’K$. Anche la sua ascensione retta e la sua declinazione sono cambiate: se $\gamma S$ era l’ascensione retta iniziale, la nuova ascensione retta è $\gamma’S’$. La declinazione, misurata inizialmente dall’arco $AS$ è diventata l’arco $AS’$. L’unica coordinata rimasta uguale è la sua latitudine eclittica, misurata dall’arco $AK$.
In seguito alla precessione annua $\psi$, una stella passa dalle coordinate equatoriali ($\alpha;\delta$) alle nuove coordinate ($\alpha’;\delta’$). Le variazioni di coordinate $\Delta\delta=\delta’-\delta$ e $\Delta\alpha=\alpha’-\alpha$ si possono calcolare con le seguenti formule, dove $\epsilon$ è l’obliquità dell’eclittica:
$$\Delta\delta=\psi \sin \epsilon \cos \alpha$$
$$\Delta\alpha=\psi( \cos \epsilon + \sin \epsilon \sin \alpha \tan \delta)$$

