Nel corso dell’anno il Sole non sorge e non tramonta sempre negli stessi punti dell’orizzonte. Il punto del sorgere e il punto del tramonto coincidono con il punto cardinale est e ovest soltanto agli equinozi di marzo e di settembre.
Al solstizio di dicembre, per un osservatore boreale il punto del sorgere raggiunge la sua massima distanza, verso Sud, rispetto al punto cardinale Est (massima amplitudine ortiva sud).
Il punto del sorgere raggiungerà la sua massima distanza, verso NORD, (massima amplitudine ortiva nord) nel giorno del solstizio di giugno.
Analogamente, il punto del tramonto si allontana dal punto cardinale OVEST raggiungendo le massime amplitudini nord e sud nei giorni dei solstizi.
L’ampiezza delle amplitudini varia con la posizione geografica.
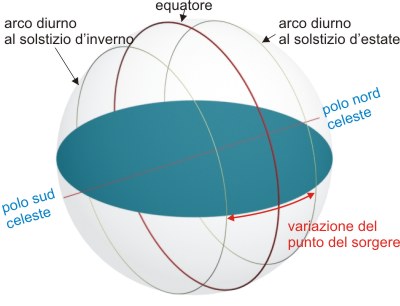
Nella figura qui sopra si rappresentano gli archi diurni del Sole ai solstizi e agli equinozi, per un osservatore posto all’equatore. A questa latutidine la distanza tra i punti del sorgere e i corrispondenti punti del tramonto tra i due solstizi è la minima possibile: circa $47^\circ$ (pari al doppio dell’obliquità dell’eclittica $2\times23^\circ\text{,5}$).

In questa figura si rappresentano gli archi diurni del Sole per un osservatore posto a circa $45^\circ$ di latitudine. L’arco di orizzonte compreso tra la massima amplitudine nord e la massima amplitudine sud è di circa $68^\circ$.

Per un osservatore posto alla latitudine del circolo polare artico il punto del sorgere spazia tra il punto cardinale Nord (“sole di mezzanotte” al solstizio d’estate) e il punto cardinale Sud (al solstizio d’inverno, quando non sorge). Quindi l’arco di orizzonte compreso tra le due amplitudini massime raggiunge i $180^\circ$. Se l’osservatore è a latitudini ancora superiori, questo arco supera i $180^\circ$ fino a raggiunge i $360^\circ$ nel caso estremo di un osservatore posto al polo nord, nel qual caso, tra l’equinozio di primavera e l’equinozio d’autunno il Sole descrive archi diurni paralleli all’orizzonte, (praticamente degli almucantarat) sempre al di sopra di esso.
Le amplitudini del Sole al suo sorgere e al suo tramontare, essendo in relazione con le lunghezze dell’arco diurno e notturno, sono legate anche alle ore di illuminazione.
Le amplitudini del Sole dipendono matematicamente dalla declinazione $\delta$ del Sole e dalla latitudine $\varphi$ del luogo e si possono calcolare con la seguente formula:
$$\boxed{\cos\widehat{Z}=\frac{\sin\delta}{\cos\varphi}}$$
dove $\widehat{Z}$ è l’angolo azimutale. Quest’ultimo ci fornisce facilmente l’amplitudine. Per chi è interessato, nella pagina seguente si dimostra questa formula.
Vedi anche: Le ore di illuminazione e fotografare le variazioni di amplitudine
Suggerisco Motions of the Sun, un’ottima simulazione che, più di tante parole, ci fa capire la relazione tra declinazione, latitudine e tempo.
- Orbita, eclittica, equatore
- Lo zodiaco: segni e costellazioni
- Stagioni
- Punto del sorgere e punto del tramonto del Sole
- Fotografare le variazioni di amplitudine
- Le ore di illuminazione
- Linea diurna e sezione conica
- Levata eliaca e tramonto eliaco
- Passaggi al meridiano e culminazioni
- Movimento apparente delle stelle circumpolari
- Moto diretto e retrogrado
- Oscillazioni dell’asse terrestre
- Aberrazione della luce
- La teoria solare tolemaica

