E’ una deviazione della direzione di vista di un astro dovuta alla combinazione del moto orbitale della Terra attorno al Sole con il moto dei fotoni provenienti dall’astro.
La parola aberrazione deriva dal latino aberrare dove ab- indica un allontanamento ed errare significa “andare vagando, senza saper dove”. L’aberrazione è perciò un “deviare dal vero, errare gravemente”. L’aberrazione della luce fa sì che un astro ci appaia in una posizione che non è quella “vera”.
L’esempio più immediato per capire il fenomeno è quello della pioggia. Immaginiamo un giorno di pioggia senza vento: la traiettoria delle gocce che cadono è verticale. Se in quel giorno facciamo un viaggio in automobile, potremo assistere al fenomeno che chiamerei “aberrazione della pioggia” osservando i finestrini laterali: le gocce non cadono verticalmente colpiscono il vetro diagonalmente: la direzione di caduta non è più verticale ma è inclinata “in avanti”.
Ciò è dovuto alla combinazione del moto dell’osservatore con il moto delle gocce di pioggia. E’ una questione di sistemi di riferimento: se si prende come riferimento il suolo, le gocce cadono verticali, se si prende come riferimento l’automobile, esse cadono oblique. Si potrà notare facilmente che la deviazione dalla verticalità aumenta con l’aumentare della velocità. L’aberrazione della luce possiede alcuni aspetti in comune con il fenomeno descritto, primo fra tutti la relatività del moto. Dobbiamo tener presente però, che mentre la pioggia scende pressoché verticale in tutto l’ambiente intorno, i fotoni raggiungono il nostro occhio da tutte le direzioni della sfera celeste.
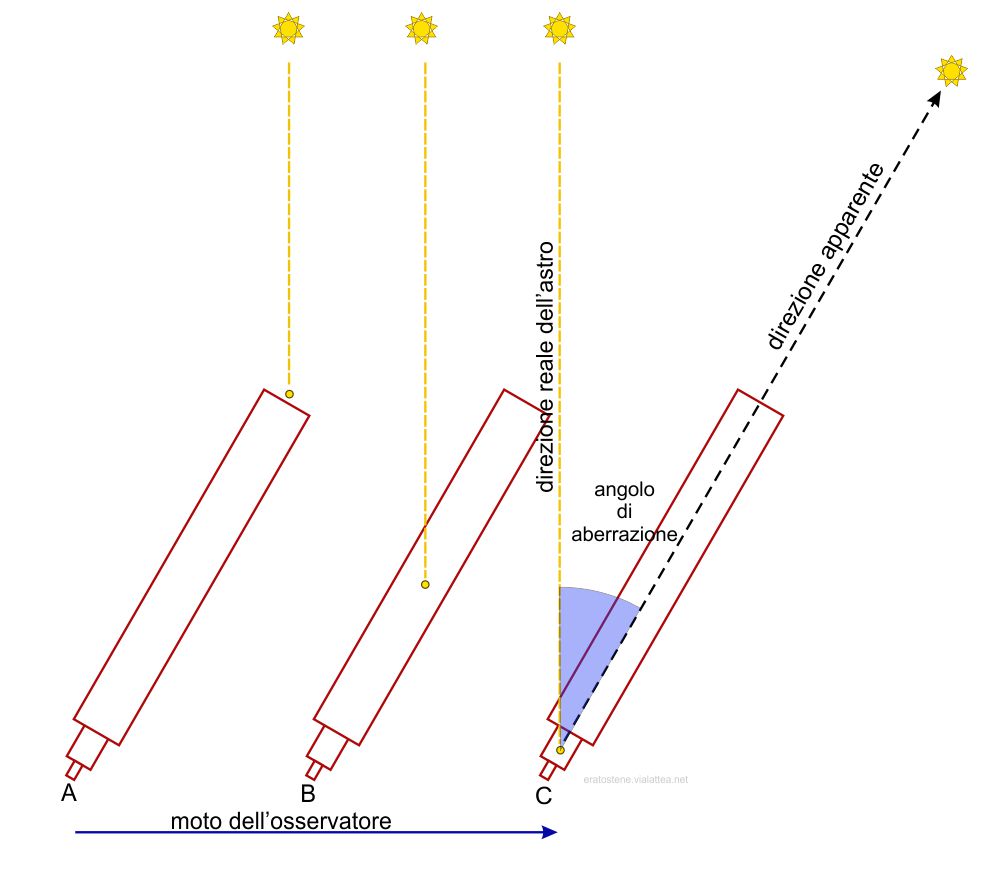
Vediamo in questo schemo cosa accade ad un astronomo che osserva una stella con il suo telescopio (gli angoli sono esagerati). Immaginiamo, per semplificare, che la stella si trovi allo zenit. Un suo fotone è rappresentato mentre scende verticalmente alla velocità di $300\,000km/s$. Nel frattempo l’osservatore si muove, con la Terra, alla velocità di quasi $30km/s$ in una certa direzione (verso destra nel nostro schema). Sono disegnati tre istanti successivi di questo moto e l’occhio dell’osservatore si trova successivamente nelle posizioni $A$, $B$ e $C$. Quando un fotone entra nell’obiettivo del telescopio, l’occhio in posizione $A$ ancora non lo vede. Non lo vede nemmeno l’occhio che arriva al punto $B$. Il fotone raggiunge l’occhio solo nella posizione $C$. Per vedere la stella, l’astronomo ha dovuto inclinare il tubo del telescopio di un certo angolo rispetto alla direzione verticale di propagazione dei fotoni. Perciò, per l’astronomo, la direzione della stella non è quella “vera” tabulata nei cataloghi stellari, ma è una direzione leggermente inclinata nel verso del moto della Terra. L’angolo compreso tra queste due direzioni si chiama angolo di aberrazione.
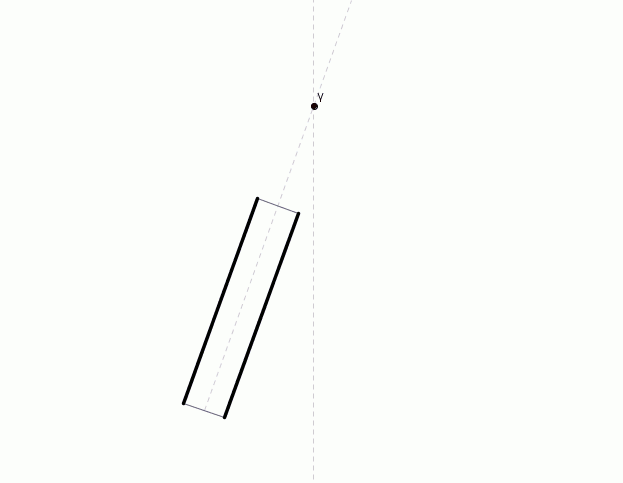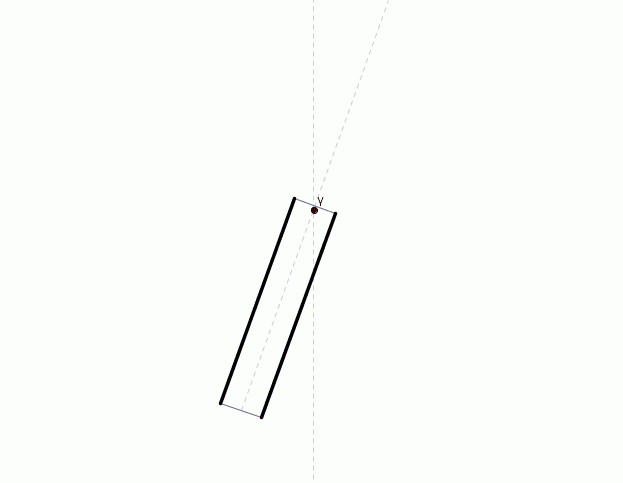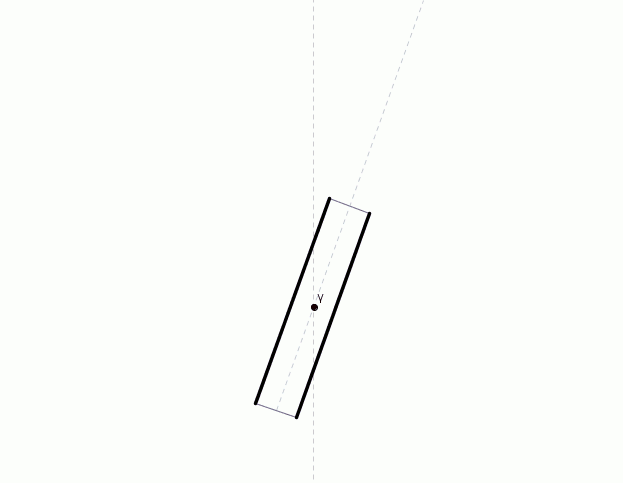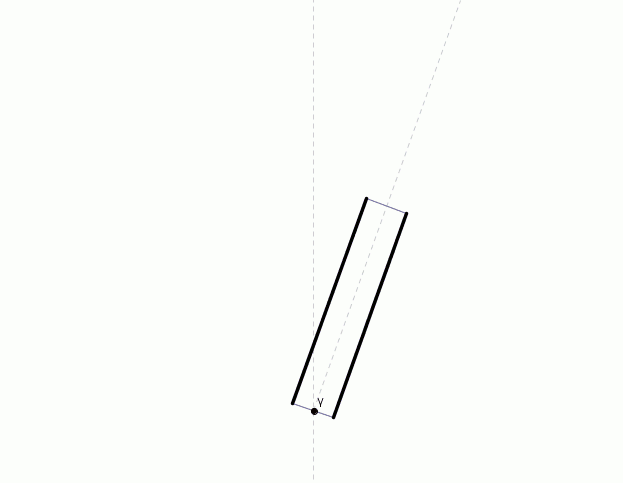
Questa semplice animazione chiarisce in pochi secondi tutta la discussione precedente. Il fotone scende verticalmente ma sembra giungere obliquamente all’occhio dell’osservatore (elaborato, da wikimedia)
Qualsiasi moto dell’osservatore provoca l’aberrazione della luce. Un osservatore terrestre ha un moto complesso dovuto alla combinazione di rotazione e di rivoluzione, ma l’aberrazione dovuta alla rotazione (aberrazione diurna) è trascurabile rispetto a quella dovuta al molto di rivoluzione (aberrazione annua).
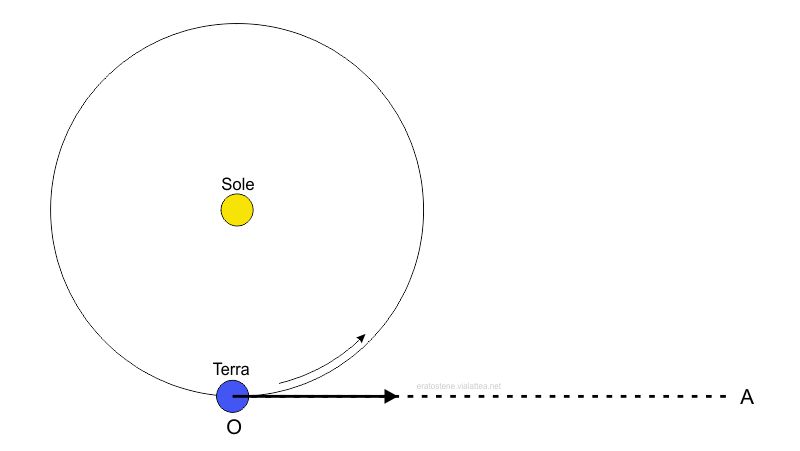
Analizziamo meglio questo secondo fenomeno. Qual è la direzione del moto della Terra in un certo istante? Il vettore del moto ha una direzione tangente all’orbita nel punto in cui si trova la Terra. Il suo verso corrisponde al senso antiorario, se visto da un osservatore che si trova al polo nord dell’eclittica. Se prolunghiamo idealmente tale vettore si raggiunge la sfera celeste nel punto A, chiamato apice del moto annuo terrestre. Esso rappresenta il punto verso il quale la Terra si sta dirigendo in quell’istante. Se semplifichiamo la forma dell’orbita ad un cerchio, l’apice si trova lungo l’eclittica, a ovest del Sole, e sempre a distanza di $90^\circ$ di longitudine celeste da esso. L’apice, ovviamente, si muove con moto diretto lungo l’eclittica, mantenendo la distanza di $90^\circ$ dal Sole. Per l’effetto dell’aberrazione delle luce, le direzioni di tutti gli astri si “inclinano” verso l’apice.
L’angolo di aberrazione $\omega$, espresso in arcosecondi, si ottiene da una semplice funzione:
$$\boxed{\omega=20,\!5^”\sin i}$$
dove $i$ è la distanza angolare dell’astro dall’apice del moto. Il valore $20,\!5^”$ è chiamato costante di aberrazione annua e indica la massima deviazione possibile della direzione di un astro. Ciò accade quando $\sin i=1$, cioè quando la distanza angolare dell’astro dall’apice del moto è di $90^\circ$.
Per chi apprezza il potere della geometria nel semplificare un problema che sembra complesso, in coda a questa pagina troverà la dimostrazione della formula.
Cosa accade alla posizione apparente delle stelle nel corso di una rivoluzione? Come si è detto dipende dalla distanaza angolare di un astro rispetto all’apice del movimento.
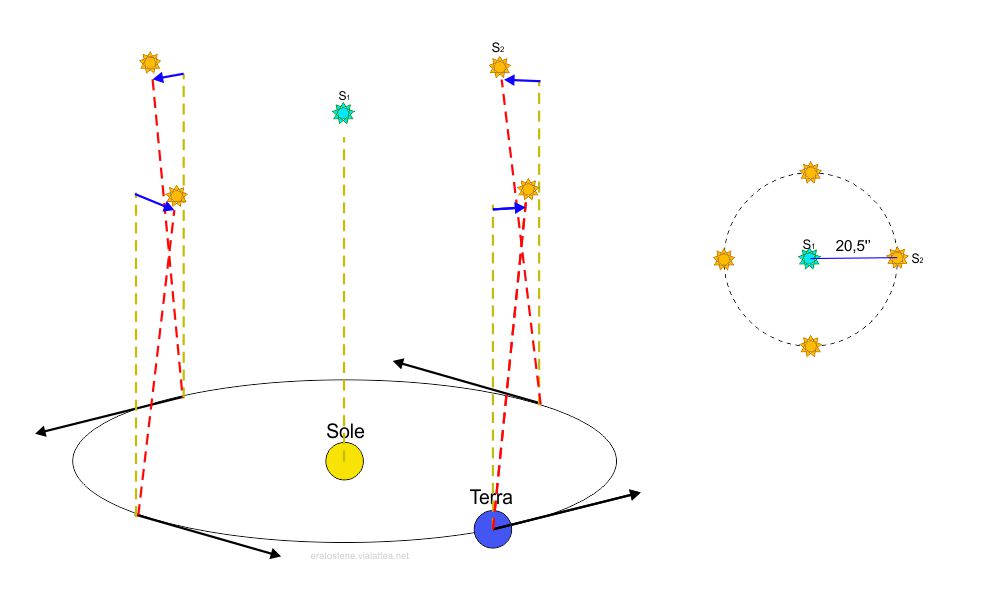
Gli astri che si trovano nei pressi del polo nord o del polo sud dell’eclittica, distano $90^\circ$ dall’apice e hanno anche una latitudine eclittica di $90^\circ$. Essi subiscono costantemente la massima deviazione ($20\text{,5}^{”}$). Tale deviazione però segue il moto apparente dell’apice che, come abbiamo detto, a sua volta segue il Sole nel suo moto apparente annuo lungo l’eclittica. La deviazione è sia in longitudine eclittica che in latitudine eclittica. In conclusione questi astri descrivono, in un anno, una circonferenza di raggio pari alla costante di aberrazione.
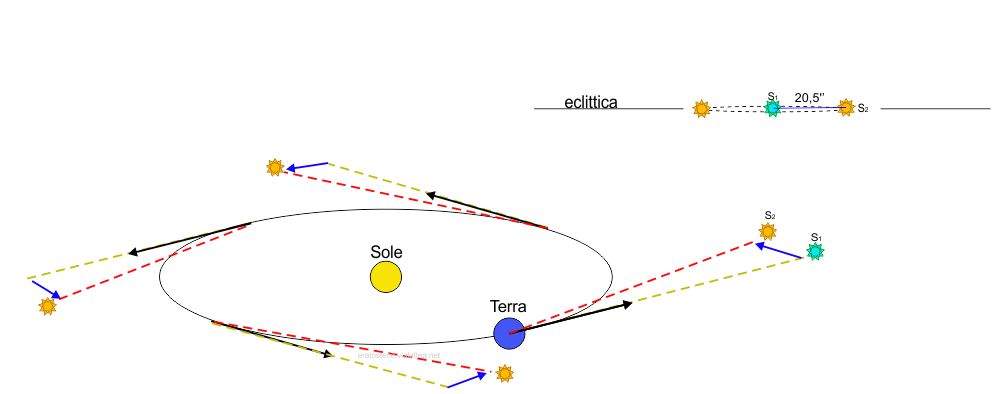
Il caso estremo opposto è quello degli astri che si trovano lungo l’eclittica. Anche la loro direzione subisce una deviazione che è sempre in direzione del Sole. Ma si tratta di un’oscillazione che è solo in longitudine eclittica, ampia complessivamente $41^”$.
Tutti gli astri che hanno latitudini eclittiche intermedie formano sempre un’ellisse, il cui semiasse maggiore è pari alla costante di aberrazione, mentre il semiasse minore varia nell’intervallo compreso tra $0^”$ e $20,\!5^”$
L’aberrazione della luce fu scoperta da James Bradley (1693–1762) nel tentativo di misurare la parallasse annua delle stelle, e annunciata alla Royal Society nel 1729. La deviazione dovuta all’aberrazione, infatti, è molto più consistente di quella dovuta alla parallasse annua (anche nel caso della stella più vicina, Proxima Centauri, la parallasse annua è di soli $\text{0,77}$ secondi d’arco). Perciò nelle misurazioni di parallasse è necessario tener conto innanzitutto dell’aberrazione. Questo è uno dei tanti esempi nella storia della scienza in cui nel tentativo di dimostrare una legge si scopre un nuovo fenomeno inaspettato. Bradley interpretò correttamente l’aberrazione che, oltre a diventare una dimostrazione del moto della Terra attorno al Sole, fu utilizzata da lui per uno dei primi tentativi di misurazione della velocità della luce.
–
Dimostrazione (classica)
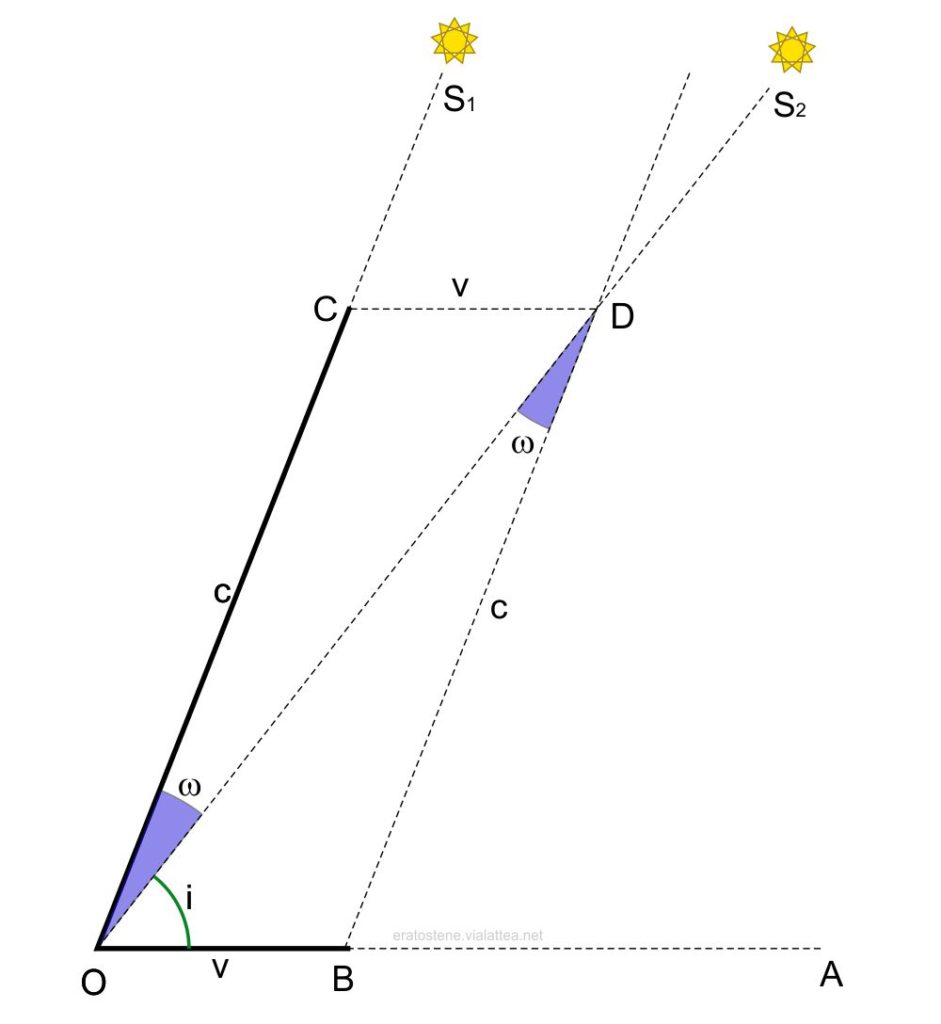
L’osservatore $O$ si muove, con la Terra, nella direzione $OA$, essendo $A$ l’apice del moto di aberrazione. La direzione $OS_1$ è quella che dovrebbe avere una stella per osservatore $O$. Ma l’osservatore è in moto: la sua velocità $v$ è rappresentata dalla lunghezza del segmento $\overline{OB}$. La velocità della luce $c$ è invece rappresentata dalla lunghezza del segmento $\overline{OC}$. In questo schema non sono conservate le proporzioni tra queste due lunghezze per motivi di chiarezza.
Si costruisca il parallelogramma $OBCD$. La direzione $OS_2$ è la direzione apparente della stella $S_1$, deviata dell’angolo $\omega$ rispetto alla direzione “reale” $OS_1$, a causa dell’aberrazione.
L’angolo $i$ rappresenta la distanza angolare della stella dall’apice $A$.
Si applichi ora il teorema dei seni al triangolo $OBD$:
$$\frac{v}{\sin\omega}=\frac{c}{\sin i}$$
da cui si ricava:
$$\sin \omega = \frac{v}{c}\cdot\sin i$$
All’angolo $\omega$ si può applicare infine l’approssimazione per angoli piccoli ($\sin\omega=\omega$) per cui:
$$\omega = \frac{v}{c}\cdot\sin i$$
ed infine, come d’abitudine per gli angoli piccoli, si può esprimere $\omega$ in arcosecondi. Un radiante vale $206\,265^”$ perciò:
$$\omega = \frac{v\cdot 206\,265^”}{c}\cdot\sin i$$
Ora, la velocità $v$ della Terra si può calcolare facilmente, approssimando la sua orbita alla forma circolare e sapendo che il raggio è la distanza media tra la Terra e il Sole ($149\,597\,871 km):
$$v = \frac{s}{t} = \frac{2\pi\,149\,597\,871\,km}{365,\!25\cdot24\cdot3600^s}=\simeq29,\!8\,km/s$$
La parte costante della formula dell’aberrazione diventa ora:
$$\frac{v\cdot206\,265^”}{c}=\frac{29,\!8\cdot206\,265^”}{299792,\!5 }=20,5^”$$
Ed ecco infine la semplice funzione che fornisce l’angolo di aberrazione $\omega$ espresso in arcosecondi:
$$\omega=\text{20,5}^”\sin i$$

