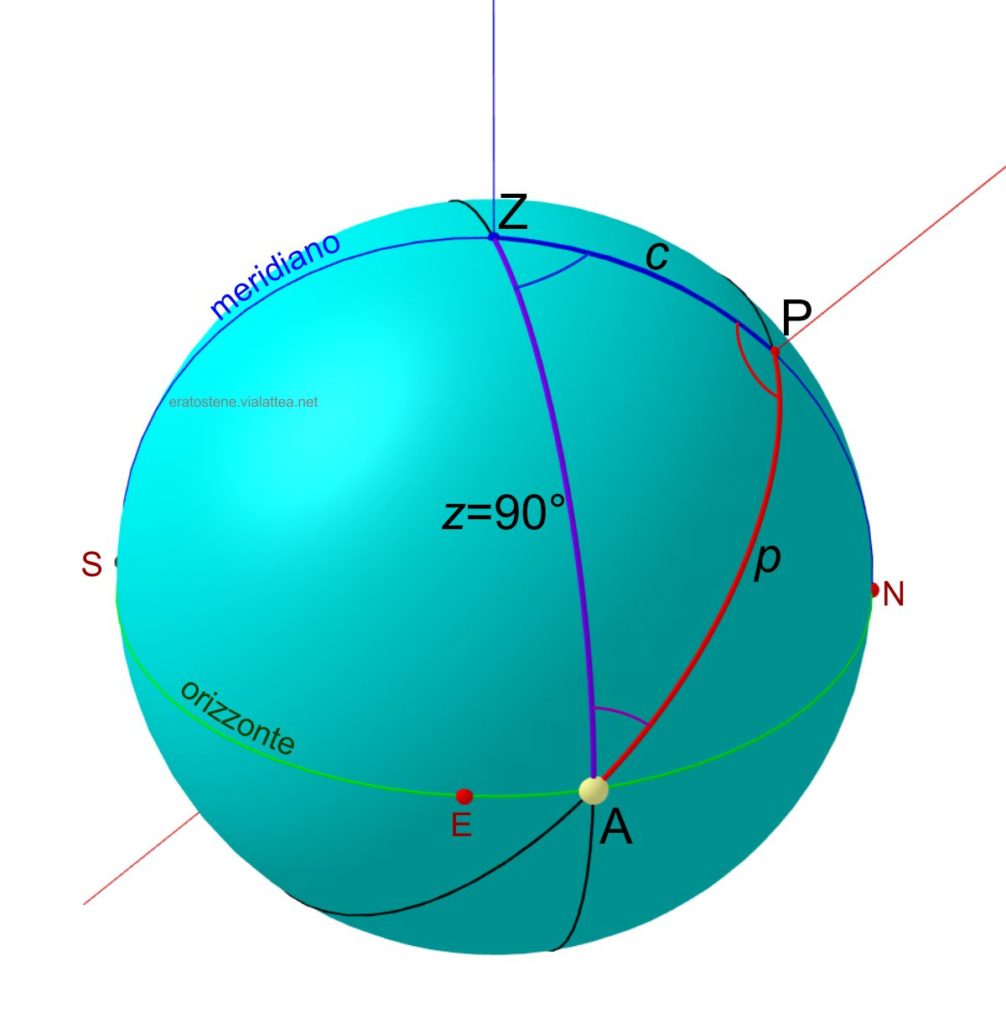
Osserviamo il triangolo sferico $ZPA$. E’ il famoso triangolo di posizione dove $Z$ è lo zenit, $P$ è il polo nord celeste e $A$ è l’astro, che nel nostro caso è il Sole all’orizzonte nel suo punto del sorgere. In questa situazione particolare il triangolo di posizione è un triangolo rettilatero perché la distanza zenitale $z$ è un arco di $90^\circ$ essendo uguale alla distanza tra lo zenit e l’orizzonte.
Ricordiamo che gli altri due lati del triangolo di posizione sono la colatitudine $c$ e la distanza polare $p$ e che gli angoli sferici sono l’angolo azimutale $\widehat{Z}$, l’angolo parallattico $\widehat{A}$ e l’angolo al polo $\widehat{P}$ .
Possiamo applicare al triangolo le regole di Nepero per calcolare $p$:
$$\cos p =\sin c \cdot \sin(90^\circ-\widehat{Z})$$
Sapendo che:
- $\sin(90^\circ-\widehat{Z})=\cos\widehat{Z}$
- $\cos p = \cos(90^\circ-\delta)=\sin\delta$
- $\sin c = \sin(90^\circ-\varphi)=\cos\varphi$
Possiamo trasformale l’uguaglianza in questo modo:
$$\sin \delta =\cos \varphi \cdot \cos\widehat{Z}$$
da cui la formula che dovevamo dimostrare:
$$\boxed{\cos\widehat{Z}=\frac{\sin \delta}{\cos \varphi}}$$

