Dimostrazione delle formule di trasformazione dalle coordinate eclittiche a quelle equatoriali
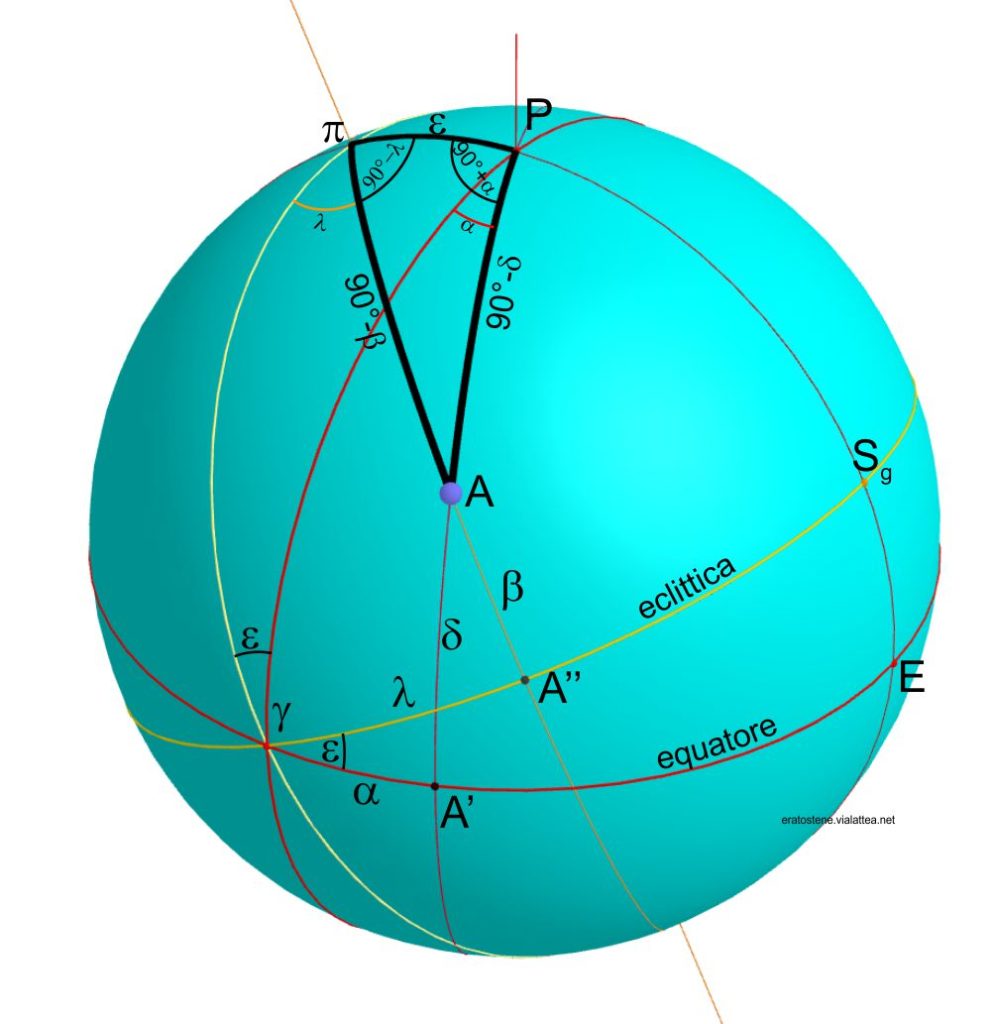
Il metodo si basa sull’applicazione delle formule fondamentali di trigonometria sferica sul triangolo sferico $\pi P A$ i cui vertici sono:
$\pi$: il polo nord dell’eclittica.
$P$: il polo nord celeste.
$A$: l’astro.
Osservando la stessa figura vediamo che questo triangolo è inserito in entrambi i sistemi di coordinate. Il semicircolo che passa per $P$, $A$, $A’$ e giunge al polo sud celeste (non visibile qui) è l’orario dell’astro $A$ mentre il semicircolo che passa per $\pi$, $A$, $A”$ e giunge al polo sud dell’eclittica è il suo meridiano di eclittica. L’orario dell’astro interseca ad angolo retto l’equatore nel punto $A’$ (piede dell’astro sull’equatore). Allo stesso modo, il meridiano dell’astro interseca l’eclittica ad angolo retto nel punto $A”$ (piede dell’astro sull’eclittica). Quindi l’arco $AA’=\delta$ è la declinazione dell’astro, mentre l’arco $AA”=\beta$ è la sua latitudine eclittica. Sul triangolo sferico $\pi P A$ troviamo i loro complementi che sono: il lato $PA=90^\circ-\delta$ e il lato $\pi A=90^\circ-\beta$.
Il circolo massimo che passa per $\pi$, $P$, $S_g$ ed $E$ è il coluro dei solstizi. $S_g$ è in fatti il punto solstiziale di giugno. Questo circolo interseca ad angolo retto altri due circoli massimi importanti: il coluro degli equinozi che passa per i punti $P$, $\gamma$, il polo sud celeste e il primo punto della Bilancia (gli ultimi due qui sono invisibili), e il circolo che passa per $\pi$, $\gamma$, il polo sud dell’eclittica e il primo punto della Bilancia. Questi circoli massimi formano, rispettivamente con l’equatore e con l’eclittica, due triangoli trirettilateri e trirettangoli: il triangolo $\pi \gamma S_g$ e il triangolo $P\gamma E$.
Il punto $\gamma$ o punto vernale, è l’origine sia dell’ascensione retta che della longitudine eclittica. L’ascensione retta $\alpha$ è l’arco di equatore $\gamma A’$ ed anche l’angolo sferico $\gamma \widehat{P}A’$.
La longitudine eclittica $\lambda$ è l’arco di eclittica $\gamma A”$ ed anche l’angolo sferico $\gamma\widehat{\pi}A”$. Di conseguenza l’angolo $A\widehat{\pi}P$ è uguale a $90^\circ-\lambda$.
Infine, l’arco $\pi P$ è l’obliquità dell’eclittica $\epsilon$. Esso rappresenta la rotazione del sistema eclitticale rispetto al sistema equatoriale attorno alla linea dei nodi che congiunge il punto gamma al primo punto della Bilancia.
Abbiamo definito cinque elementi del triangolo sferico. Il sesto elemento, l’angolo $\pi \widehat{A} P$ non ci sarà utile.
Ora siamo pronti ad applicare al triangolo sferico $\pi P A$ i teoremi fondamentali, nell’ordine, il teorema del coseno, il teorema dei seni e il teorema delle proiezioni, che riportiamo qui nello loro forma generica:
\begin{align*}
\cos{a}&=\cos{b}\cdot\cos{c}+\sin{b}\cdot\sin{c}\cdot\cos{\alpha} \\
\sin a\cdot\sin \beta &=\sin{\alpha}\cdot\sin{b}\\
\sin a \cdot \cos \beta &= \cos b \cdot \sin c – \sin b\cdot\cos c \cdot \cos \alpha
\end{align*}

Lo schema a fianco aiuterà la sostituzione degli elementi delle formule generiche (quelle esterne colorate in rosso) con i corrispondenti elementi del triangolo $\pi P A$.
Il risultato è questo:
$\cos{(90^\circ-\delta)}=\cos{(90^\circ-\beta)}\cdot\cos{\epsilon}+\sin{(90^\circ-\beta)}\cdot\sin{\epsilon}\cdot\cos{(90^\circ-\lambda)}$
$\sin{(90^\circ-\delta)}\cdot \sin{(90^\circ+\alpha)}= \sin{(90^\circ-\beta)} \cdot \sin{(90^\circ-\lambda)}$
$\sin (90^\circ-\delta) \cdot \cos (90^\circ+\alpha) = \cos (90^\circ-\beta) \cdot \sin \epsilon- \sin(90^\circ-\beta)\cdot\cos \epsilon \cdot \cos (90^\circ-\lambda)$
Semplifichiamo ora le tre uguaglianze applicando alcune semplici regole trigonometriche. La prima uguaglianza si trasforma così nella formula che permette calcolare la declinazione conoscendo le due coordinate eclittiche e l’obliquità dell’eclittica:
\begin{equation}\tag{1}
\boxed{\sin{\delta}=\sin{\beta}\cdot\cos{\epsilon}+\cos{\beta}\cdot\sin{\epsilon}\cdot\sin{\lambda} }
\end{equation}
Le altre due uguaglianze servono per ottenere la seconda formula con qualche elaborazione:
Infatti, dividendo membro a membro la seconda uguaglianza con la prima ottenendo:
\begin{align*}
\cos{\delta}\cdot \cos{\alpha}&= \cos{\beta} \cdot \cos{\lambda}\\
-\cos \delta \cdot \sin \alpha &= \sin \beta \cdot \sin \epsilon – \cos\beta\cdot\cos \epsilon \cdot \sin\lambda
\end{align*}
$$\tan\alpha=\frac{\cos\beta\cdot\cos \epsilon \cdot \sin\lambda – \sin \beta \cdot \sin \epsilon}{\cos{\beta} \cdot \cos{\lambda}}$$
Semplifichiamo ancora dividendo per $\cos\beta$ sia il numeratore che il denominatore della frazione al secondo membro, ottenendo infine la formula per calcolare l’ascensione retta che volevamo dimostrare:
\begin{equation}\tag{2}
\boxed{\tan\alpha=\frac{\cos \epsilon \cdot \sin\lambda – \tan \beta \cdot \sin \epsilon}{\cos{\lambda}}}
\end{equation}

Un procedimento molto simile, direi speculare, ci permette di dimostrare le formule di trasformazione inversa. Non riportiamo qui la dimostrazione che lasciamo ai lettori desiderosi di esercitarsi. Suggeriamo soltanto di utilizzare le stesse formule generali ma di seguire questo nuovo schema di sostituzione in cui, rispetto al precedente, abbiamo scambiato tra loro le posizioni dei lati $a$ e $b$ e degli angoli $\alpha$ e $\beta$.

