Dimostrazione delle formule di trasformazione dalle coordinate altazimutali a quelle orarie
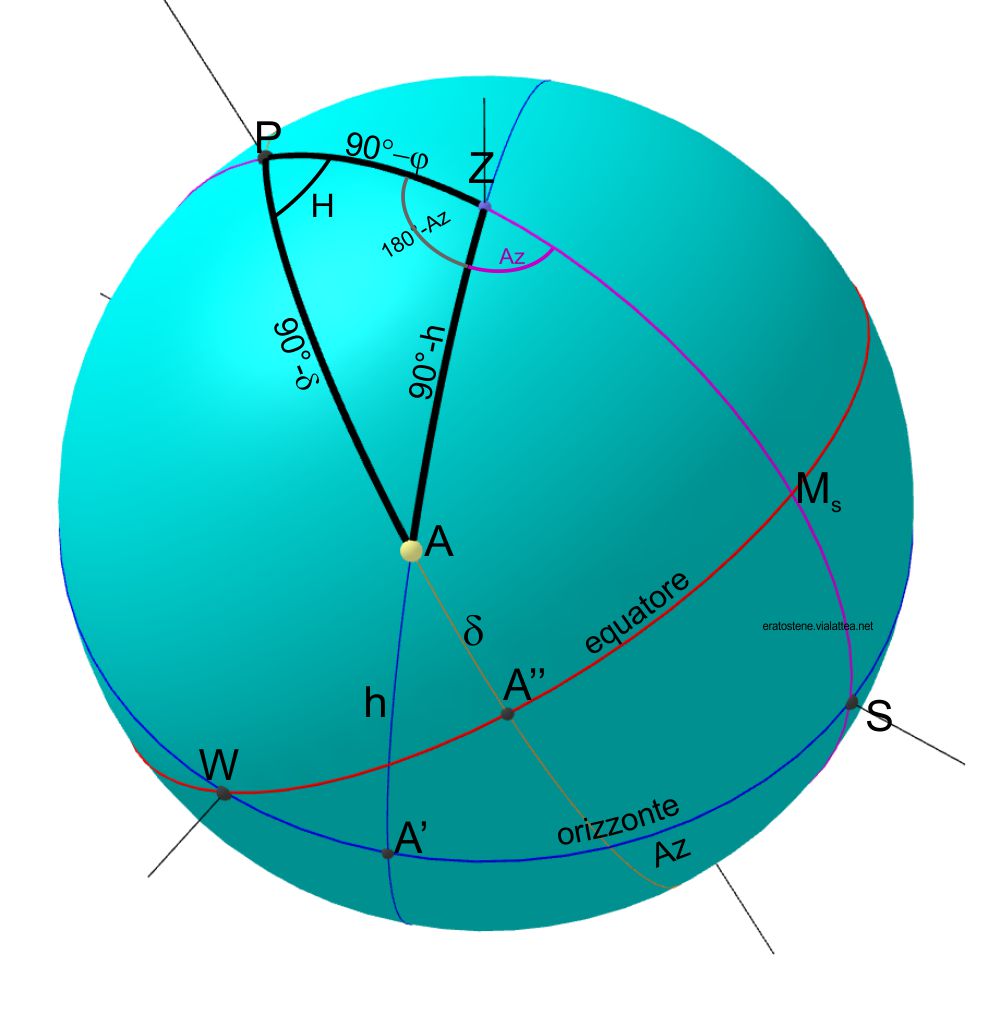
La dimostrazione si ottiene applicando i teoremi fondamentali della trigonometria sferica al triangolo sferico $AZP$, noto come triangolo di posizione dove $P$ è il polo celeste nord, $Z$ è lo zenit e la posizione dell’astro è il terzo vertice $A$.
L’equatore e l’orizzonte sono inclinati tra loro di un angolo pari alla colatitudine $90^\circ-\varphi$, dove $\varphi$ è la latitudine; nella nostra figura la colatitudine è rappresetata dall’arco $PZ$ che è uno dei lati del triangolo di posizione, dall’arco $M_sS$ dove $M_s$ è il mezzocielo superiore e $S$ è il punto cardinale sud, e anche dall’angolo sferico $M_s\widehat{W}S$ dove $W$ è il punto cardinale ovest. Il circolo massimo $PZM_sS$ è il meridiano celeste, che contiene il semicircolo di origine sia per l’azimut che per l’angolo orario.
Il semicircolo che passa per $P$, $A$, $A”$ e per il polo celeste sud (che qui è invisibile) è l’orario dell’astro $A$. Esso interseca l’equatore ad angolo retto nel punto $A”$ che è il piede dell’astro sull’equatore. L’arco $AA”$ è la declinazione di $A$. Essendo l’arco $PAA”=90^\circ$, il lato $PA$ del triangolo di posizione, noto come distanza polare, è complementare alla declinazione: $PA=90^\circ-\delta$. Una descrizione analoga va fatta per l’altezza $h$ uguale all’arco $AA’$ che fa parte del verticale dell’astro ($A’$ è il piede dell’astro sull’orizzonte). Il lato $ZA$ è noto come distanza zenitale ed è complementare all’altezza. Perciò: $ZA=90^\circ-h$.
L’angolo orario $H$, in questo schema, è rappresentato sia dall’arco di equatore $M_sA”$ e anche dall’angolo sferico $A\widehat{P}Z$ del triangolo di posizione, noto come angolo al polo. L’azimut $A_z$ del nostro schema, contato a partire da sud, è l’arco di orizzonte $A’S$ ma anche l’angolo sferico $A’\widehat{Z}S$. Perciò, l’angolo sferico $P\widehat{Z}A$, noto come angolo azimutale, è supplementare all’azimut misurato da sud: $P\widehat{Z}A=180^\circ-A_z$.
Ora siamo pronti ad applicare al triangolo sferico $ZP A$ i teoremi fondamentali, nell’ordine, il teorema del coseno, il teorema dei seni e il teorema delle proiezioni, che riportiamo qui nella loro forma generica:
\begin{align*}
\cos{a}&=\cos{b}\cdot\cos{c}+\sin{b}\cdot\sin{c}\cdot\cos{\alpha} \\
\sin a\cdot\sin \beta &=\sin{\alpha}\cdot\sin{b}\\
\sin a \cdot \cos \beta &= \cos b \cdot \sin c – \sin b\cdot\cos c \cdot \cos \alpha
\end{align*}
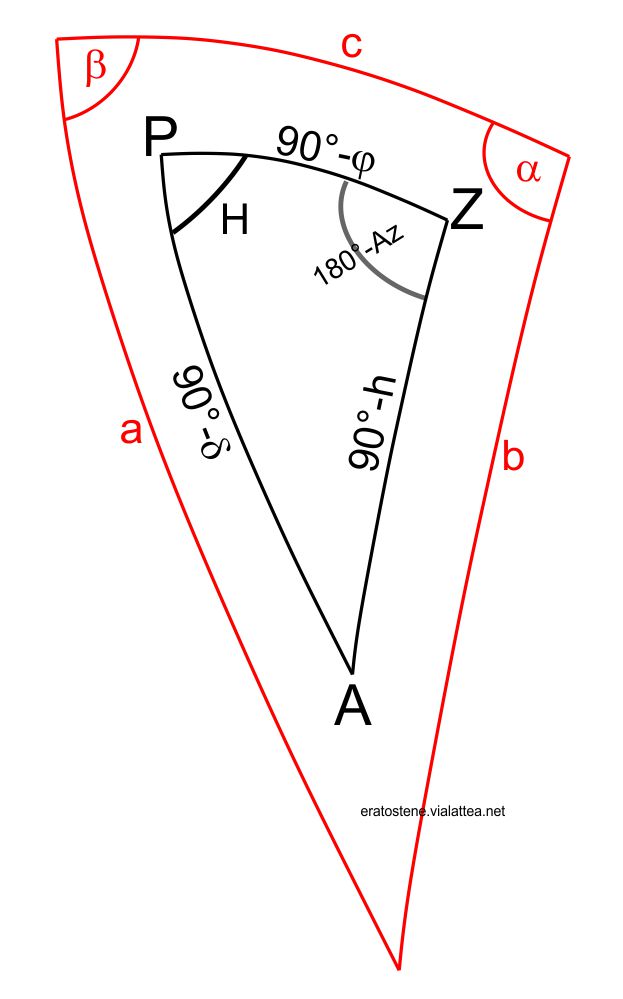
Per prima cosa eseguiamo la “traduzione” dei simboli generici sostituendoli con gli elementi del nostro triangolo di posizione. Questo schema ci può aiutare.
Le tre formule diventano:
$$\cos{(90^\circ-\delta)}=\cos{(90^\circ-h)}\cdot\cos{(90^\circ-\varphi)}+\sin{(90^\circ-h)}\cdot\sin{(90^\circ-\varphi)}\cdot\cos{(180^\circ-A_z)}$$
$$\sin{(90^\circ-\delta)}\cdot \sin{H}= \sin{(90^\circ-h)} \cdot \sin{(180^\circ-A_z)}$$
$$\sin (90^\circ-\delta) \cdot \cos H = \cos (90^\circ-h) \cdot \sin(90^\circ- \varphi) – \sin (90^\circ-h)\cdot\cos(90^\circ- \varphi) \cdot \cos (180^\circ-A_z)$$
Semplifichiamo ora le tre uguaglianze seguendo alcune semplici regole trigonometriche. La prima uguaglianza si trasforma così nella formula che volevamo dimostrare e che permette di calcolare la declinazione in funzione delle coordinate altazimutali e della latitudine:
\begin{equation}\tag{1}
\boxed{
\sin{\delta}=\sin{h}\cdot\sin{\varphi}-\cos{h}\cdot\cos{\varphi}\cdot\cos A_z
}
\end{equation}
Le altre due uguaglianze diventano:
$$\cos{\delta}\cdot \sin{H}= \cos{h} \cdot \sin A_z$$
$$\cos \delta \cdot \cos H = \sin h \cdot \cos \varphi + \cos h\cdot\sin \varphi \cdot \cos A_z$$
e dividendo membro a membro la prima con la seconda si ottiene:
$$\tan H=\frac{\cos h\cdot\sin A_z}{\sin h\cdot \cos \varphi + \cos h\cdot\sin\varphi\cdot\cos A_z}$$
Infine semplifichiamo dividendo per $\cos h$ sia il numeratore che il denominatore del secondo membro. Otteniamo così la formula che permette di calcolare l’angolo orario in funzione delle coordinate altazimutali e della latitudine dell’osservatore:
\begin{equation}\tag{2}
\boxed{
\tan H=\frac{\sin A_z}{\tan h\cdot \cos \varphi + \sin\varphi\cdot\cos A_z}
}
\end{equation}
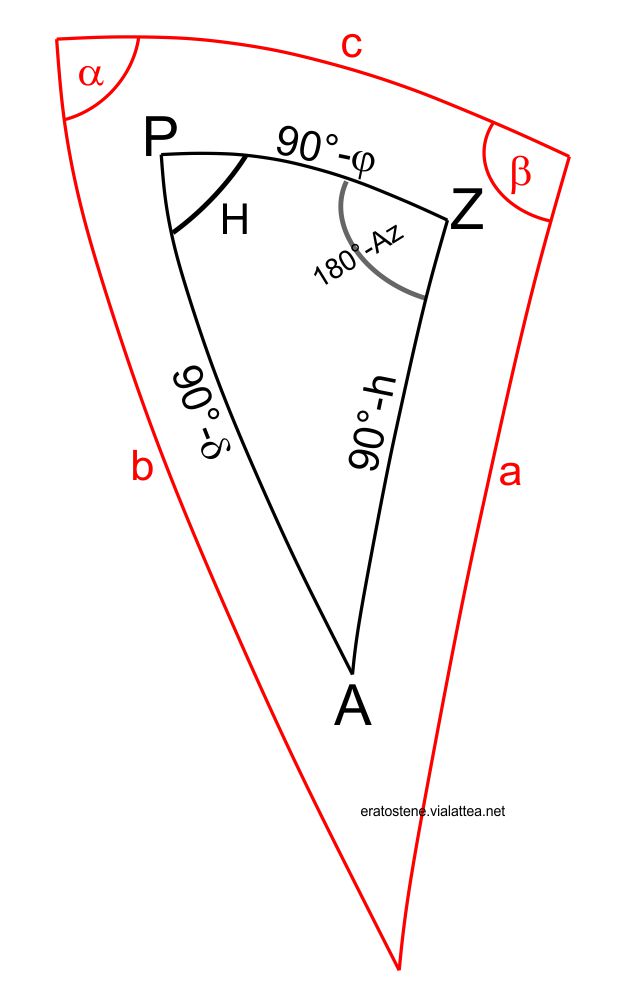
La dimostrazione delle formule inverse è molto simile: cambia solo la modalità di “traduzione” degli elementi generici dei teoremi fondamentali. Lasciamo questo compito ai lettori che desiderano esercitarsi. Suggeriamo soltanto lo schema qui a fianco in cui, rispetto al precedente, sono stati scambiati tra loro i nomi dei lati $a$ e $b$ e i nomi degli angoli $\alpha$ e $\beta$.

